1. Rational Bias

Problem: Given a data sequence, e.g. ACGTAGCAGATAGACAGGTTAGACAATAGAG, and a "bias" criterion, e.g. "at least 2/3 AT-rich", find the longest contiguous interval (substring) that satisfies this criterion.

In the HTML-form below, the fraction is p/q where p and q are small integers which (for given p and q) yields a simple, special-case, linear-time algorithm (but the multiplier depends on p and q).

key: `choice' -- acceptable characters. `p' and `q' -- p/q is the required fraction of acceptable characters.

2. General Bias

Give elements of the sequence a +ve value for "good" and a -ve value for "bad". Compute the cumulative sums from the start of the sequence. The sum of a "good enough" interval is non-negative, i.e. the cumulative sum is flat or increasing across the interval:

e.g. required ratio = 1/2

cum' sum:	(solid black) the cumulative sum
first below:	tracks the 1st point where the cum' sum falls to certain value
last above:	tracks the last point at which the cum' sum holds a certain value (can be computed in a reverse scan of cum' sum)
candidates:	(dashed) indicate some possible ``longest biased intervals''

(All) Longest Biased Intervals:

(I.e. find every biased interval that is not strictly contained in any other biased interval.)

If the required minimum fraction (bias) is `x', where 0<=x<=1, give "good" elements a weight of +(1-x) and "bad" elements a weight of -x. (NB. x need not be rational.)

Step along `last-above' from top-left to bottom-right (thus R.H. end of interval always advances) while

looking back at first-below.

The longest biased interval of all will be discovered by this process.

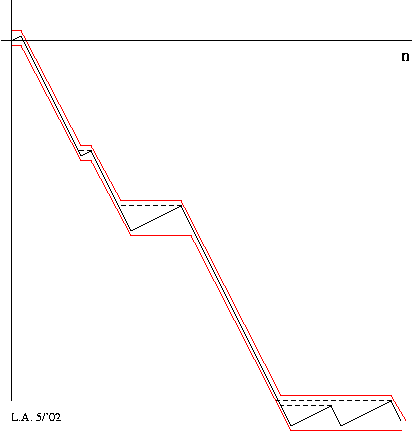
e.g. required ratio = 2/3 (good = +1/3, bad = -2/3)

The following HTML-form implements a general algorithm for biases that are not necessarily rational. Its time-complexity is almost always O(n), but can be O(n²) in the worst case for ``pathalogical'' sequences.

Note that some numbers, including some common rational numbers, cannot be represented exactly in floating-point. Therefore one might need to give `ratio' a (very, very,) very little ``slack''.

3. Notes

Using binary-search to search (track) the array of cumulative-sum minima would give an O(n.log(n))-time, O(n)-space algorithm.

So of course, one could run both algorithms in parallel and take the result from the first to finish (also halting the other one): O(n)-time usually and O(n.log(n))-time worst case [11 April 2003].

4. Reference

L. Allison, Longest Biased Interval and Longest Non-Negative Sum Interval, Bioinformatics, 19(10), pp.1294-1295, 1 July 2003.