Heap Sort

Heap sort forces a certain property onto an array which makes it into what is known as a heap. The elements of the array can be thought of as lying in a tree structure:

Heap
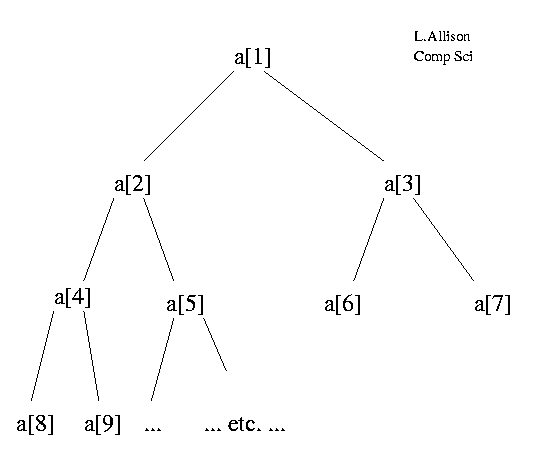
--- Array as a Heap ---

The children of a[i] are a[2*i] and a[2*i+1]. The tree structure is purely notional; there are no pointers etc.. Note that the array indices run through the "nodes" in breadth-first order, i.e. parent, children, grand-children,....

An array a[i..j] is called a heap if the value of each element is greater than or equal to the values of its children, if any. Clearly, if a[1..N] is heap, then a[1] is the largest element of the array.

Now, if a[k+1..N] is a heap, a[k..N] can be made into a heap efficiently: 

downHeap(int a[], int k, int N)
/*  PRE: a[k+1..N] is a heap */
/* POST:  a[k..N]  is a heap */
 { int newElt, child;
   newElt=a[k];
   while(k <= N/2)   /* k has child(s) */
    { child = 2*k;
      /* pick larger child */
      if(child < N && a[child] < a[child+1])
         child++;
      if(newElt >= a[child]) break;
      /* else */
      a[k] = a[child]; /* move child up */
      k = child;
    }
   a[k] = newElt;
 }/*downHeap*/

This operation moves the new element, a[k], down the heap, moving larger children up, until the new element can be placed in such a way as to maintain the heap property. The heap can have "height" at most log2(N), so the operation takes at most O(log(N)) time.

Heap Sort

This now leads to a version of heap sort known as (bottom-up) heap sort:

heapSort(int a[], int N)
/* sort a[1..N],  N.B. 1 to N */
 { int i, temp;
   for(i=N/2; i >= 1; i--)
      downHeap(a, i, N);
   /* a[1..N] is now a heap */

   for(i=N; i >  1; i--)
    { temp = a[i];
      a[i]=a[1]; /* largest of a[1..i] */
      a[1]=temp;

      downHeap(a,1,i-1); /* restore a[1..i-1] heap */
    }
 }/*heapSort*/
L
.
A
l
l
i
s
o
n

Heap Sort Demonstration

Change the data in the HTML FORM below, click `go', and experiment. The portion of the array that is a heap is bracketted [...] in the trace. You can see the heap grow during the first phase and shrink during the second phase:

input:  
output:
trace:  
stat's: 

Exercises

  1. For a given value of N, e.g. N=6, find input data that maximises the number of comparisons that the algorithm makes.
  2. For a given value of N, e.g. N=6, find input data that minimises the number of comparisons that the algorithm makes.

Complexity

Time

Heap sort makes at most 1.5*N calls on downHeap. DownHeap makes at most log(N) iterations, and each iteration makes two comparisons, so heap sort makes at most 3*N*log(N) comparisons. It can be shown than bottom up heap sort actually makes at most 2*N*log(N) comparisons. Its worst and average case time-complexity is O(N*log(N)).

Space

Heap Sort's space-complexity is O(1), just a few scalar variables.

Stability

Heap sort is not stable.

Notes

L. A.©