Tries

A trie (from retrieval), is a multi-way tree structure useful for storing strings over an alphabet. It has been used to store large dictionaries of English (say) words in spelling-checking programs and in natural-language "understanding" programs. Given the data:

an, ant, all, allot, alloy, aloe, are, ate, be

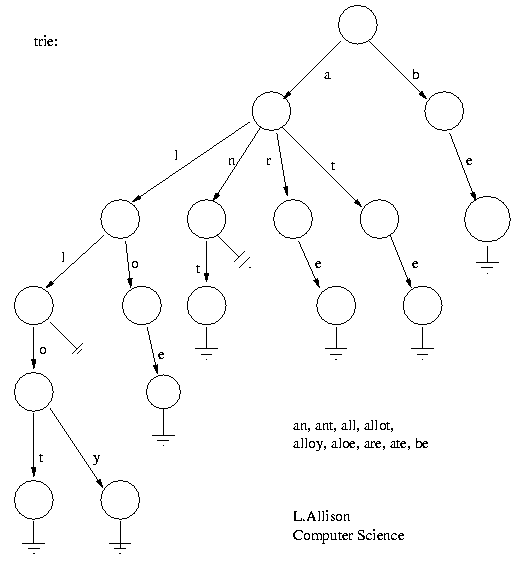
The idea is that all strings sharing a common stem or prefix hang off a common node. When the strings are words over {a..z}, a node has at most 27 children - one for each letter plus a terminator.

The elements in a string can be recovered in a scan from the root to the leaf that ends a string. All strings in the trie can be recovered by a depth-first scan of the tree.

One fast but rather wasteful way to implement a trie in Pascal:

type trie = ^ node;
     node = record
               subtrie :array['a'..'z'] of trie;
               IsEndOfWord :boolean
            end;

It is wasteful as a lot of nodes near the edge of the trie will have most subtries set to nil. On the other hand lookup is direct as there is random access on each level/character position in a string.

function find(word:string; length:integer; t:trie):boolean;

   function f(level:integer; t:trie):boolean;
   begin if level=length+1 then
            f:=t^.IsEndOfWord
         else if t^.subtrie[word[level]]=nil then
            f:=false
         else f:=f(level+1, t^.subtrie[word[level]])
   end{f};

begin find := f( 1, t )
end{find}

A second way to implement the trie is to represent each node in the trie as a linked-list of at most 27 elements, each element being a pair <char,trie>. In this case, a search (linear, binary, ...) must be used at each level but less space is wasted at leaves; remember most trees have more leaves than forks.

Notes

• The height of a trie is the length of the longest key in the trie.
• E. Fredkin. Trie Memory. Comm. ACM 3(9) pp490-499 Sept. 1960.
• See [PATRICIA trees].
• See [Suffix Trees] for string searching etc..