Appeared in Nucleic Acids Research (NAR) / Computer Applications in the Biosciences (CABIOS) special issue, CABIOS 4(1) pp.97-101, Jan. 1988, (now 'Bioinformatics') [doi:10.1093/bioinformatics/4.1.97]

L. Allison & C. N. Yee, Department of Computer Science, Monash University, Clayton, Victoria, Australia 3168.

Written: 29^th July 1987; revised: 27^th October.

Abstract: A computer algorithm for restriction-site mapping consists of a generator of partial maps and a consistency checker. This paper examines consistency checking and argues that a method based on separation theory extracts the maximum amount of information from fragment lengths in digest data. It results in the minimum number of false maps being generated.

Introduction.

Restriction-site mapping involves locating certain restriction sites on a circular plasmid, on a linear phage or on some other sequence of DNA. The raw data for the problem consist of fragment lengths from one or more digests carried out on the DNA. Deducing the map is a combinatorial problem often performed with the aid of a computer program [1-9]. While there is only one real map, the data can suggest several, perhaps a great many, maps particularly when experimental errors are considered. It is very important that no map consistent with the data is missed. It is almost equally important that every effort be taken to suppress inconsistent maps which could swamp the experimenter.

This paper examines the problem of placing the strongest constraints, that can be deduced from the experimental data, on maps being generated by a computer program. The measured fragment lengths place limits on the distances between sites. Given single and double digests, there are multiple limits between each pair of sites. These limits form a network or graph of connections between the sites and fall into a class of inequalities known as separation theory [10]. Such a graph can be checked for consistency by checking each simple cycle in the graph. Results given later show the degree of rejection of false maps in a mapping program which uses separation theory. Given n sites, there are O(n²) simple cycles to check but it is also shown that a compromise algorithm checking only O(n) cycles is nearly as stringent as the full check. For simplicity, the tests are performed on two enzyme, single and double, total digest data; the constraint checking method described can be incorporated in programs that handle more complex data.

Generation.

A restriction-site mapping algorithm consists of two logically independent components. A generator builds partial maps and a constraint checker validates or rejects these maps [7]. In a given program the two components may be intertwined but logically they are quite separate. Generation amounts to permuting the fragments indicated by the experimental data. As the number of permutations grows exponentially with the number of fragments, the strictest possible constraints should be checked as soon as practicable on partial maps so as to reduce the amount of time taken. Algorithms that generate complete permutations and only then examine them for consistency are restricted to small problems [5].

If there is an unbroken run of three or more sites of one kind, and hence of two or more digest fragments of one kind, the digest data cannot distinguish between the permutations of these fragments. The generator can suppress multiple solutions in this case and generate one candidate map only [6]. Similarly, symmetries should be suppressed. If a map is produced its reflection, and in the case of a circular map its rotations, should not be generated.

Separation Theory.

This section describes a method of constraint checking for the restriction-site mapping problem. It is based on Pratt's separation theory [10] and extracts the maximum possible amount of information from fragment lengths in the digest data. It will also be shown that the constraint checking adopted by some other algorithms is a weaker subset or a special case of the method described here.

The simplest application will be described in which there are only two enzymes and in which their single and double digests are performed. The method can be generalized to data from more than two enzymes.

There are many sources of error in digest data, for example:

1. Short fragments may be lost.

2. Two fragments of similar size may appear as a single fragment.

3. Digestion may be incomplete.

4. There are errors in estimating fragment lengths.

For the time being it is assumed that the only errors are in estimating fragment lengths and that an upper bound on this error is known.

With the above assumptions, a fragment length represents a range of possible lengths, [lo,hi], between some lower limit and some higher limit. It can be thought of as a rod or link in a child's construction set, with an elongated hole at one end representing the uncertainty in its length:

 --------------------------------------------
 | o                            =========== |
 --------------------------------------------

   |<--------estimated length------->|
                                     |<-->|
                                |<-->|
                                  +-error
   |<-------------- lo -------->|
   |<------------------- hi ------------->|

When a map is assembled from the fragments (or links), the errors lead to uncertainty in the positions of sites, but the two single digest maps and the double digest map must be consistent.

 Single digest 1, Enzyme 1:

  ... --------A1----A2--------------A3---------- ...


 Double digest, Enzyme 1+Enzyme 2:

  ... --B1----A1----A2-----B2-------A3------B3-- ...


 Single digest 2, Enzyme 2:

  ... --B1-----------------B2---------------B3-- ...

Drawing the double digest map in a slightly different way yields this picture:

 Enzyme 1
             A1------A2             A3
            .          .           .  .
           .            .        .      .
          .              .     .          .
         .                .  .              .
  ... --B1                 B2                B3-- ...
 Enzyme 2

Note, the map is one dimensional; it has been drawn in two dimensions for reasons that will become apparent.

There must be a digest 1 fragment for A2-A3, digest 2 fragments for B1-B2 and for B2-B3, both a digest 1 and a double digest fragment for A1-A2, and double digest fragments (only) for B1-A1, A2-B2, B2-A3 and A3-B3. Drawing all these fragments on one composite map yields:

 Enzyme 1
  ... ------A1=====A2------------- A3 ----------- ...
           .         .           .    .
          .           .        .        .
         .             .     .            .
        .               .  .                .
  ... -B1----------------B2------------------B3-- ...
 Enzyme 2

The result is a graph or network of points {A1, A2, A3, B1, B2, B3, ...} and edges or links between some of them. Each edge defines limits on the distances between two points of the form:

      lo <= P-Q <= hi
 or   Q <= P - lo   and   P <= Q + hi

The coefficients of the variables, P and Q, are 1 and each inequality involves exactly two variables. Checking a set of inequalities of this kind for consistency falls directly into separation theory [10].

It can be seen that the graph above provides alternative paths between any two points. For example, A2-B2-B3 and A2-A3-B3 are two paths from A2 to B3. Such a pair of paths form a loop or a cycle when joined together, eg. A2-B2-B3-A3-A2. If the cycle does not cross itself, as in this case, it is called a simple cycle.

Returning to the two paths, A2-B2-B3 and A2-A3-B3, traversing each path amounts to selecting certain single and double digest fragments. Since the end points, A2 and B3, are fixed points on a molecule, the sums of the lengths of the fragments on each path must be consistent. That is, the range of lengths implied by each path must overlap. The lower (upper) limit of a path is the sum of the lower (upper) limits of its fragments. Two paths are inconsistent if the upper limit of one is less than the lower limit of the other, otherwise they are consistent:

    [-----]       [------]     [------]        [---]
 [----]      or       [----] or  [--]    or  [--------]

Separation theory shows that to check a graph for consistency, it is necessary and sufficient to check each simple cycle for consistency.

In the particular graphs relevant to restriction-site mapping, it is sufficient to find all pairs of points <L,R> where L is to the left and R to the right. There is one simple cycle with L as its extreme left point and R as its extreme right point. There are two paths (forming the simple cycle) from L to R - an upper one and a lower one. All such pairs of paths must be consistent for the map to be consistent with the experimental data.

Checking the paths described extracts all the information in the digest data. Note that the checks can easily be applied to partial maps that are in the process of being built; only new cycles need be checked when a map is extended.

Examples.

Sometimes adjacent sites in a map are of the same kind, for example:

               [lo1,hi1]
  ........ A1==============A2 ........
               [lo3,hi3]

There are two paths A1-A2 - there must be a digest 1 fragment [lo1,hi1] and a double digest fragment [lo3,hi3]. For consistency lo1<=hi3 and lo3<=hi1. In this case, the two fragments, constraints or links can be replaced by one stricter fragment, constraint or link: [max(lo1,lo3),min(hi1,hi3)].

Sometimes sites alternate:

                  B1
               .     .   [lo4,hi4]
  [lo3,hi3] .           .
         .                .
  ...  B1------------------B2 ....
              [lo2,hi2]

There must be a digest 2 fragment [lo2,hi2] and double digest fragments [lo3,hi3] and [lo4,hi4]. [lo2,hi2] and [lo3+lo4,hi3+hi4] must be consistent.

Note that it is possible for 2 partial maps to be individually consistent but for them to be mutually inconsistent:

                                       [219-230]
             A1                  A1----------------A2
            .  .                   .              .
 [90,100].        .[109,120] [109,120].        .[90-100]
      .              .                   .  .
    B1----------------B2                  B2
          [190,200]

The map for {A1,B1,B2} is consistent and implies that A1-B2 is in the range [max(190-100, 109), min(200-90, 120)] = [109,110]. The map for {A1,B2,A2} is consistent and implies that A1-B2 is in the range [max(219-100, 109), min(230-90,120)] = [119,120]. The two partial maps cannot be reconciled. This can be seen by comparing the paths B1-A1-A2 in the range [309,330] and B1-B2-A2 in the range [280,300] which are inconsistent:

                      [219,230]
              A1--------------------A2
            .    .                .
 [90,100] .          .         . [90,100]
        .                .  .
      B1------------------B2
               [190,200]

Note that while the errors for long paths accumulate, it is nevertheless possible for discrepancies along alternative long paths to "tighten up", even rejecting a map as here.

Other Algorithms.

Nolan, Maina and Szalay [4] describe a mapping algorithm based on forks. For each single digest fragment, a search is made for sets of double digest fragments that it might consist of. Such a set of fragments is called a fork. They build single digest maps using the forks to check for consistency were fragments on the two single digest maps overlay each other. It can be seen that forks correspond to just the smallest, indivisible cycles in the graph described previously. There are possible benefits in that the forks algorithm checks fewer constraints which may save time. On the other hand, the fewer constraints may lead to many false solutions (see last example of previous section) which may waste time.

The constraints checked by Fitch, Smith and Ralph's algorithm [3] and by Dix and Kieronska's algorithm [1] are indivisible cycles also.

Some other algorithms appear to check only the partial lengths of the two single digest maps and the double digest map as they are being built. This corresponds to checking just those cycles that pass through the extreme left-hand point of the graph.

Using Other Constraints and Heuristics.

To use a computer algorithm correctly a clear understanding of its parameters is needed. The separation theory algorithm takes each error bound on a fragment length to be an absolute limit which may not be exceeded. An experimenter may therefore wish to estimate these bounds conservatively. It may be that an experimenter would accept a solution in which one limit were just exceeded but in which all others were comfortably accommodated. In that case the experimenter must increase the estimated errors accordingly.

It might appear that some other algorithms previously mentioned are less severe in excluding possible maps and that this might be a good thing. However there is an element of arbitrariness in which constraints they choose to enforce. If a map happens to exceed one constraint that is checked, it will be excluded. The separation theory method is entirely evenhanded in applying all constraints implicit in the digest data. Given a realistic upper limit on errors it accepts exactly those maps consistent with the data.

It is possible to incorporate other heuristics with this algorithm. Separation theory examines discrepancies in distances between all pairs of sites. Other counters can be kept and used to reject possible maps. For example, predicted digest data can be compared with the experimental data and a "sum of the squares of the differences" [5] can be calculated. If this exceeds some limit the map can be rejected. The limit can be set by previous solutions using "branch and bound" [3].

In the case of a circular map, a final check must be performed on each solution that the total lengths of the two single digest maps and of the double digest map are consistent.

As mentioned previously, there are several sources of error in digest data over and above uncertainty in fragment lengths. These are really outside the scope of this paper and do not affect the constraint checker; most can be accommodated by the generator algorithm. Two fragments of similar length may show as a single fragment. Often there is a clue to this problem but it can be programmed around by the generator being able to choose fragments more than once, subject to the total lengths of the maps being consistent. Incomplete digestion can be dealt with by allowing the generator to omit certain fragments.

Most mapping problems involve several enzymes. All single digests, several double digests and maybe some triple digests are performed. The separation theory method provides cross-referencing constraints between any two single digests and their double digest. The method can clearly be extended to problems with more than two enzymes.

Results.

A number of constraint checkers for restriction site mapping, including the separation theory checker, were programmed in the Mu-Prolog dialect [11] of the Prolog [12] programming language. Prolog is based on logic and is particularly suitable for combinatorial problems; although it is usually interpreted and therefore slow.

It is notoriously difficult to measure the average behaviour of combinatorial algorithms that are highly data dependent. To compare the algorithms, the approach was taken of using the worst kind of data that could reasonably be expected to arise naturally. This consists of "rather a lot" of sites of just two enzymes. Algorithms will behave poorly on such data because of the exponential growth of the number of permutations of each kind of fragment and because of the relatively small amount of cross-referencing information between only two single and one double digest. The pertinent statistic for constraint checkers is the number of solution maps they allow versus the error bound in the data. For simplicity the percentage error was varied over each set of fragment lengths; in reality the error depends on fragment length in a more complex way.

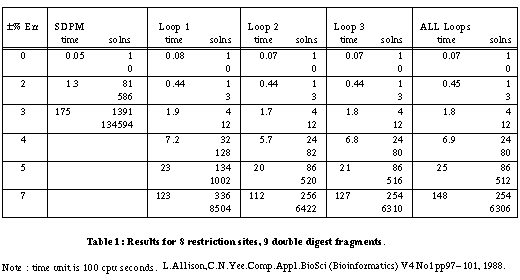
Table 1 gives the results for a linear mapping problem on 8 restriction sites and 9 double digest fragments. The error varies up to ±7%. The times should be treated with great caution as they depend on the computer, the language and the generator algorithm. (Since this paper was first written, the algorithms have been coded in Pascal and run approximately 60 times faster.) The SDPM column is for a simple algorithm which checks only the overall lengths of partial maps. The Loop 1, Loop 2 and Loop 3 columns are for checking restricted numbers of cycles - 1, 2 and 3 respectively. Loop 1 checks indivisible cycles and corresponds to forks. Loop 2 also checks cycles that contain two indivisible cycles and so on. The All Loops column is for the full separation theory check on all simple cycles.

Table 1

There are two figures for numbers of solutions. The first is the number of unique maps for the two kinds of site. Each map may be "confirmed" by several permutations of the double digest fragments. The second figure indicates this excess.

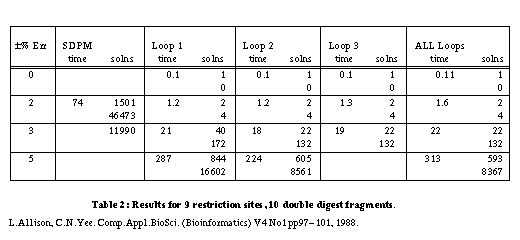
Table 2 gives some results for a larger problem with 9 sites and 10 fragments.

Table 2

A constraint checker is called to apply tests to partial maps during the search for solutions. When a constraint is violated, all extensions of the partial map are ignored. As might be expected, the constraints of the smallest, indivisible cycles are violated most frequently. Of the maps that do pass these tests, the constraints for next shortest cycles containing two indivisible cycles are violated most frequently and so on. With 9 sites and ±3% error, checking 1 cycle gives 40 solutions; checking all cycles gives 22 solutions. In general there are diminishing returns for checking more and more cycles - see 8 sites and ±7% error. A reasonable compromise in terms of the number of false maps rejected versus the time taken is to check only those simple cycles containing 1, 2 or 3 indivisible cycles. This almost always yields the minimum number of maps generated in a near minimum search time.

References.

[1] Dix T. I., Kieronska D. H. (1987) Proceedings 10^th Australian Computer Science Conference, Deakin University, 37-45.

[2] Durand R., Bregere F. (1984) Nucl. Acids Res. 12 703-716.

[3] Fitch W. M., Smith T. F., Ralph W. W. (1983) Gene 22 19-29.

[4] Nolan G. P., Maina C. V., Szalay A. A. (1984) Nucl. Acids Res. 12 717-729.

[5] Pearson W. R. (1982) Nucl. Acids Res. 10 217-227.

[6] Polner G., Dorgai L., Orosz L. (1984) Nucl. Acids Res. 12 227-236.

[7] Stefik M. (1978) Artificial Intelligence 11 85-114.

[8] Stone B. N., Griesinger G. L., Modelevsky J. L. (1984) Nucl. Acids Res. 12 465-471.

[9] Zehetner G., Lehrach H. (1986) Nucl. Acids Res. 14 335--349.

[10] Shostak R. (1981) J. Assoc. Comput. Mach. 28 769-779.

[11] Naish L. (1983) Mu-Prolog Reference Manual, Melbourne University.

[12] Clocksin W. F., Mellish C. S. (1981) Programming in Prolog. Springer Verlag.

Also see: L. Allison, T. I. Dix & C. N. Yee, Shortest Path and Closure Algorithms for Banded Matrices, Inf. Proc. Lett., 40, pp317-322, 30 Dec 1991.