Graphs

A graph G=<V,E> consists of a set of vertices (also known as nodes) V and a set of edges (also known as arcs) E. An edge connects two vertices u and v; v is said to be adjacent to u. In a directed graph, each edge has a sense of direction from u to v and is written as an ordered pair <u,v> or u->v. In an undirected graph, an edge has no sense of direction and is written as an unordered pair {u,v} or u<->v. An undirected graph can be represented by a directed graph if every undirected edge {u,v} is represented by two directed edges <u,v> and <v,u>.

A path in G is a sequence of vertices <v₀, v₁, v₂, ..., v_n> such that <v_i,v_i+1> (or {v_i,v_i+1}), for each i from 0 to n-1, is an edge in G. The path is simple if no two vertices are identical. The path is a cycle if v₀=v_n. The path is a simple cycle if v₀=v_n and no other two vertices are identical.

Graphs are useful for representing networks and maps of roads, railways, airline routes, pipe systems, telephone lines, electrical connections, prerequisites amongst courses, dependencies amongst tasks in a manufacturing system and a host of other data. There are a large number of important results and structures that are computed from graphs. Note that a rooted tree is a special kind of directed graph and that an unrooted tree is a special kind of undirected graph.

Graphs by Adjacency Matrices.

A graph G= can be represented by a |V|*|V| adjacency matrix A. If G is directed, A_ij=true if and only if <v_i,v_j> is in E. There are at most |V|² edges in E.

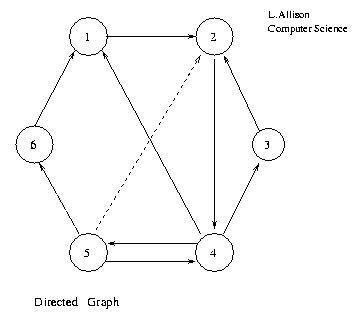
     1  2  3  4  5  6
1       T
2             T
3       T
4    T     T     T
5       T     T     T
6    T

Adjacency Matrix of Directed Graph.

If G is undirected, A_ij=A_ji=true if {v_i,v_j} is in E and A_ij=A_ji=false otherwise. In this case there are at most |V|*(|V|+1)/2 edges in E, A is symmetric and space can be saved by storing only the upper triangular part A_ij for i>=j.

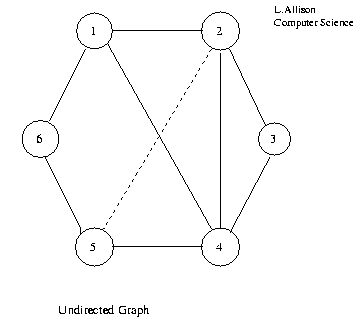
     1  2  3  4  5  6
1       T     T     T
2    T     T  T  T
3       T     T
4    T  T  T     T
5       T     T     T
6    T           T

Adjacency Matrix of Undirected Graph.

     1  2  3  4  5  6
1       T     T     T
2          T  T  T
3             T
4                T
5                   T
6

Upper Triangular Adjacency Matrix of Undirected Graph.

An adjacency matrix is easily implemented as an array.

Both directed and undirected graphs may be weighted. A weight is attached to each edge. This may be used to represent the distance between two cities, the flight time, the cost of the fare, the electrical capacity of a cable or some other quantity associated with the edge. The weight is sometimes called the length of the edge, particularly when the graph represents a map of some kind. The weight or length of a path or a cycle is the sum of the weights or lengths of its component edges. Algorithms to find shortest paths in a graph are given later.

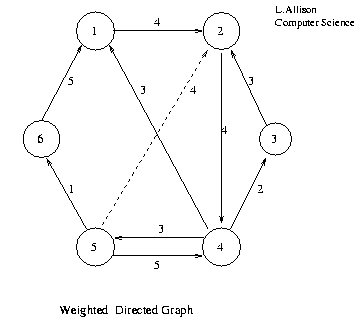
The adjacency matrix of a weighted graph can be used to store the weights of the edges. If an edge is missing a special value, perhaps a negative value, zero or a large value to represent "infinity", indicates this fact.

     1  2  3  4  5  6
1       4
2             4
3       3
4    3     2     3
5       4     5     1
6    5

Adjacency Matrix of Weighted Directed Graph.

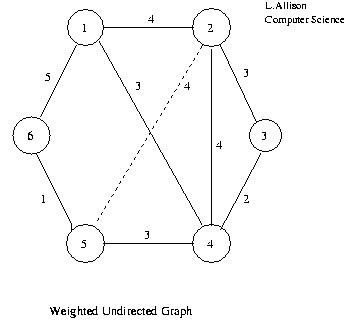
     1  2  3  4  5  6
1       4     3     5
2    4     3  4  4
3       3     2
4    3  4  2     3
5       4     3     1
6    5           1

Adjacency Matrix of Weighted Undirected Graph.

     1  2  3  4  5  6
1       4     3     5
2          3  4  4
3             2
4                3
5                   1
6

Upper Triangular Adjacency Matrix of Weighted Undirected Graph.

It is often the case that if the weights represent distances then the natural distance from v_i to itself is zero and the diagonal elements of the matrix are given this value.

A weighted adjacency matrix is easily defined in any imperative programming language.

A graph is complete if all possible edges are present. It is dense if most of the possible edges are present. It is sparse if most of them are absent, |E|<<|V|². Adjacency matrices are space efficient for dense graphs but inefficient for sparse graphs when most of the entries represent missing edges. Adjacency lists use less space for sparse graphs.

Graphs by Adjacency Lists.

In a sparse directed graph, |E|<<|V|². In a sparse undirected graph |E|<<|V|*(|V|-1)/2. Most of the possible edges are missing and space can be saved by storing only those edges that are present, using linked [lists].

Consider the weighted directed case.

An edge <v_i,v_j> is placed in a list associated with v_i. The edge is represented by the destination v_j and the weight.

1:--------->2,4:nil
2:--------->4,4:nil
3:--------->2,3:nil
4:--------->1,3:----->3,2:----->5,3:nil
5:--------->4,5:----->6,1:nil
6:--------->1,5:nil

Adjacency Lists for Weighted Directed Graph.

Consider now the undirected case:

1:--------->2,4:----->4,3:----->6,5:nil
2:--------->1,4:-----:3,3:----->4,4:----->5,4:nil
3:--------->2,3:----->4,2:nil
4:--------->1,3:----->2,4:----->3,2:----->5,3:nil
5:--------->2,4:----->4,3:----->6,1:nil
6:--------->1,5:----->5,1:nil

Adjacency Lists for Weighted Undirected Graph.

As before, half the space can be saved by only storing {v_i,v_j} for i>=j:

1:--------->2,4:----->4,3:----->6,5:nil
2:--------->3,3:----->4,4:----->5,4:nil
3:--------->4,2:nil
4:--------->5,3:nil
5:--------->6,1:nil
6:nil

Reduced Adjacency Lists for Weighted Undirected Graph.

Adjacency lists can be defined using records (structs) and pointers.

Note that some questions, such as "are v_i and v_j adjacent in G", take more time to answer using adjacency lists than using an adjacency matrix as the latter gives random access to all possible edges.

Path Problems in Directed Graphs

The weight of an edge in a directed graph is often thought of as its length. The length of a path <v₀, v₁, ..., v_n> is the sum of the lengths of all component edges <v_i,v_i+1>. Finding the shortest paths between vertices in a graph is an important class of problem.

See the [directed graph page].

Directed Acyclic Graphs

A directed acyclic graph (DAG!) is a directed graph that contains no cycles. A rooted tree is a special kind of DAG and a DAG is a special kind of directed graph.

See the [directed acyclic graph page].

The Minimum Spanning Tree of an Undirected Graph

A minimum spanning tree, T, of an undirected graph, G=<V,E>, is a tree such that:

1. T contains exactly the same vertices, V, as the graph
2. T's edges are a subset of E and
3. the total edge-weight of T is as small as possible.

See the [undirected graph page].

Exercises

1. Add to Dijkstra's algorithm so that it prints the shortest path (not just its length) between v₁ and a given vertex v_i. Hint: take note of Prim's algorithm.
2. Implement an adjacency list version of Dijkstra's algorithm. Use a [heap] as a priority queue to find the next vertex to add at each stage. This makes the algorithm O(E*log(V)). This is better than O(|V|²) for sparse graphs.
3. Compare the running time of Floyd's algorithm with running the given version of Dijkstra's algorithm |V| times to calculate all-pairs shortest paths.
4. Add to Floyd's algorithm so that it prints the shortest path (not just its length) between any two given vertices v_i and v_j.
5. Implement the topological sort algorithm for DAGs represented by adjacency lists.
6. Show how the depth-first traversal algorithm can be used to generate efficient machine code from a DAG representing an expression with common subexpressions identified. Take the target machine to be a stack machine which also has random access memory.
7. Compare the running times of Prim's and Kruskal's algorithms for graphs with various numbers of vertices, while varying the sparseness of the graphs.
8. (From the 1990 A.C.M. programming competition.) The problem is to discover an unknown collating sequence, that is a non-standard ordering of the alphabet {a..z}. You are given a list of words in an unusual alphabetic order. Write a program to discover the underlying ordering of the alphabet a-z. Assume that there is sufficient information to determine the ordering uniquely. Note that there may be letters that do not begin any word in the list.