Encoding Rooted (strict-) Binary Trees

A ‘strict binary tree’, where every node either has two subtrees (is a Fork), or has zero subtrees (is a Leaf), can be encoded in 1-bit per edge:

Perform a prefix traversal of the tree,

output 'F' for a Fork, 'L' for a Leaf,

i.e.,

data Tree = Leaf | Fork Tree Tree   -- data type defn

code Leaf = "L"

code (Fork Left Right) = "F" ++ code Left ++ code Right

e.g.,

F L F F L L L

 

Note that the method gives a prefix-code for trees; the end of the string for a tree can be detected when #L=#F+1. It is reasonable to give L and F 1-bit codes because the numbers of Ls and Fs are approximately equal.

The tree can be reconstructed from the traversal.

 

Note that encoding then decoding preserves the ordering of sub-trees from left to right; if this is unnecessary a shorter encoding must be possible (it should be possible to save 2 bits for the example above).

 

The method can be extended to non-binary trees provided the degree of each node is known, for example, if this is a known constant, or if the degrees are also encoded. For a tree of constant degree k, #L=(k-1)×#F+1 (so the code-word lengths depend on k).

 

This method of encoding trees has been used in Minimum Message Length (MML) inference for decision- (classification-) trees, and as the basis of a universal code for positive integers.

Encoding Rooted n-ary Trees.

Arbitrary n-ary trees can be encoded in about 2-bits per edge:

Perform a prefix traversal of the tree,

output 'd', for down, when descending an edge, and

output 'u', for up, when returning up an edge.

i.e.

data NTree = Leaf | Fork [NTree]

code Leaf = ""

code (Fork []) = error "not allowed"

code (Fork ts) = concat(map (\t -> 'd' ++ code t ++ 'u') ts)

e.g.,

tree as above,

d u d d d u d u u d u u

 

Each edge corresponds to one 'd' and one 'u'.

The encoding requires about 2-bits per edge.

The method applies to trees of any degree.

 

The method gives a prefix-code for trees provided that the end of the string can be detected; the end can be indicated by appending an extra 'u' because the root has no ancestor,

d u d d d u d u u d u u u

this is unnecessary if the degree of the root is otherwise known.

The tree can be reconstructed from the traversal.

 

Note that encoding then decoding preserves the ordering of sub-trees from left to right; if this is unnecessary a shorter encoding must be possible.

 

Also see generating (enumerating) sequences of n pairs of matched brackets (parentheses); think 'd' = '(', and 'u' = ')'.

Unrooted n-ary Trees

An unrooted n-ary tree can be encoded by choosing an arbitrary vertex (node) as the root and then encoding the tree as a rooted tree. This transmits log₂|V|-bits of extra information which can be subtracted.

OuterPlanar Graphs

An outerplanar graph can be drawn in the plane so that its vertices lie on a circle; some edges may run along the circle, and other edges may run across the interior of the circle without intersecting.

A tree is an outerplanar graph, and an outerplanar graph is a planar graph.

Encoding Planar Graphs (Plane Graphs)

A plane graph (a planar graph embedded in the plane) can be encoded in about 4-bits per edge [Tur84], in fact in log₂(14) bits per edge [Via08].

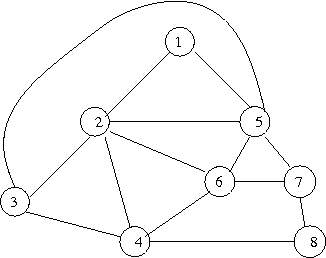
graph (after [Tur84])

 

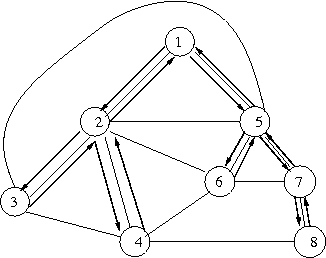
with spanning tree & traversal (bold arrows),

encoding of spanning tree: d d u d u u d d u d d u u u

 

Sweeping around each vertex anti-clockwise,

encode each "cross-tree" edge by  ( . . . ),  e.g.,

vertex	1		2		3		2		4		2		1		5		6		5		7		8		7		5		1
s.tree		d		d		u		d		u		u		d		d		u		d		d		u		u		u
other					((				)((		((				)		))(				)		)				)

all: d d ( ( u d ) ( ( u ( ( u d ) d ) ) ( u d ) d ) u u ) u

(appending an extra 'u', say, would mark the end of the encoding).

 

The numbers of ‘d’s and ‘u’s are approximately equal, the numbers of (s and )s are equal, and the blandest assumption is that the numbers of ‘u’s and (s will be about the same. The alphabet {d, u, (, )} has size 4 (2-bit codes), and each edge, of either kind, corresponds to two letters (4-bits). Any known skew in the alphabet could be used to give better compression.

 

Loops and multi-edges can be encoded.

 

The graph is planar so edges do not cross. The graph can be reconstructed by reconstructing the spanning tree, as before, and matching up corresponding (s and )s in a last-in, first-out manner.

 

[Via08] tightened up the encoding (log₂14 < 4) by recognising that certain combinations cannot be produced in the encoding.

 

Note that the construction encodes more than the planar graph -- it encodes a particular embedding of the graph in the plane, a plane graph. It also distinguishes the start ("root") vertex; log₂|V|-bits can be saved if this is arbitrary.

 

If it is possible that the graph is not connected, the number of connected components must be encoded followed by each connected component as above.

Chemical Compounds

Chemical compounds can be treated as graphs, each vertex labelled with a chemical element, and each edge labelled with a chemical bond type (single | double | triple | aromatic | hydrogen). These chemical compound graphs can be compressed and the information content of one compound given another can be calculated [All14] to give a notion of their similarity.

General Graphs

G = ⟨V, E⟩

 

If self-loops (⟨v_i,v_i⟩) and multi-edges are not allowed, an

Undirected Graph has |V|×(|V|-1)/2 possible edges,

the adjacency matrix can be coded in that many bits if pr(⟨v_i,v_j⟩ exists)=0.5 ∀i,j>i,

and a

Directed Graph has |V|×(|V|-1) possible edges,

the adjacency matrix can be coded in that many bits if pr(⟨v_i,v_j⟩ exists)=0.5 ∀i,j≠i.

 

The binomial distribution can be used to encode (rows of) an adjacency matrix if the probability of edge existence varies from graph to graph. There could be one density parameter per graph, or one parameter per row (or column) of the adjacency matrix.

 

If G is sparse, one may be tempted to encode the adjacency-lists representation. In fact the adjacency list of a vertex contains exactly the same information, and has the same message length [All18], as the corresponding row of the adjacency matrix -- see method 4 (sparse list) under the binomial distribution.

(Similar considerations apply to a dense graph.)

Regular-enough subgraphs, once identified, imply certain edges do or do not exist, e.g.,

	Km	Km',m''		. . .
Km	1s	?		?
Km',m''	?	0s	1s	?
		1s	0s
. . .	?	?		?

(if K_m',m'' disallows within-part edges)

To be worthwhile, the saving on edges must outweigh the cost of encoding the membership of a subgraph.

Finding such subgraphs is hard.

If the vertex ordering is arbitrary, any special subgraphs might as well come first and it is only necessary to encode their kinds and sizes. If the vertex ordering is not arbitrary, it takes about log ^|V|C_m bits to specify the members of K_m, for example.

Motifs

If a graph is "sufficiently regular" [Tur84], or if it contains repeated motifs, it must be possible to obtain a more efficient encoding of the graph [All18] using this fact.

E.g., [FM95] suggest that if a graph contains a bipartite clique, K_m,n, the m×n edges of the b.clique can be replaced by a new "special vertex" and m+n edges involving it. This transformation, G↔G', results in a graph, G', that has more vertices and fewer edges (is sparser) but it is not necessarily compressible unless K_m,n subgraphs are frequent in G compared to "random" graphs, and any compression might be had more directly. Finding maximal bipartite cliques is hard, but finding large ones quickly may suffice. Other "regular" subgraphs, if frequent in G, could be used for the same purpose.

Discovering general motifs that occur "frequently" in a given graph is challenging and there are many issues to consider such as whether or not instances of motifs may overlap or not. These can be resolved and used to to compress a graph [All18].

Notes

[All14] L. Allison, On the complexity of graphs (networks) by information content, and conditional (mutual) information given other graphs, TR #2014/277, FIT, Monash University, May 2014  [www (click)].

 

[All18] L. Allison, 'Graphs', Ch.11 in Coding Ockham's Razor, Springer, 2018  [doi:10.1007/978-3-319-76433-7_11]].

 

[FM95] T. Feder & R. Motwani, Clique partitions, graph compression and speeding up algorithms, Jrnl. Comp. and Sys. Sci., 51(2), pp.261-272, 1995.

 

[Tur84] G. Turan, On the succinct representation of graphs, Discr. Applied Maths., 8, pp.289-294, 1984.

 

[Via08] R. Viana, Quick encoding of plane graphs in log₂(14) bits per edge, Inf. Proc. Lett., 108, pp.150-154, 2008.

(L.A., 2008, updated 2018, 2020.)