A Bit-String Longest-Common-Subsequence Algorithm
Inf. Proc. Lett., Vol.23, Dec. 1986, pp.305-310, [doi:10.1016/0020-0190(86)90091-8].
L. Allison*, T.I. Dix*, Department of Computer Science, University of Western Australia, Nedlands, Western Australia 6009.
Abstract: A longest-common-subsequence algorithm is described which operates in terms of bit or bit-string operations. It offers a speedup of the order of the word-length on a conventional computer.
Keywords: longest common subsequence, edit distance, bit string
1. Introduction
The longest-common-subsequence (LCS) problem is to find the maximum possible length of a common subsequence of two strings, 'a' of length |a| and 'b' of length |b|. Usually an actual LCS is also required. For example, using the alphabet A, C, G and T of genetic bases, an LCS of 'GCTAT' and 'CGATTA' is 'GTT' of length three.
Here an algorithm which requires O(|a|*|b|) operations on single bits or O(ceiling(|a|/w)*|b|) operations on w-bit computer words or O(|b|) operations on |a|-bit bit-strings, for a fixed finite alphabet, is presented. Although falling into the same complexity class as simple LCS algorithms, if w is greater than any additional multiplicative cost, this algorithm will be faster. If |a|<=w the algorithm is effectively linear in |b|. (An alphabet larger than |b| can be effectively reduced to |b| by sorting 'b' in time O(|b|*log(|b|)) and using index positions in the sorted string.)
The LCS problem is related to the edit-distance [11] or evolutionary-distance problem [9] [10] where the minimum cost of editing string 'a' to string 'b' must be found. The elementary edit operations are to insert or delete one character or to change one character. There is a cost function, d(.,.), which can be extended to strings in the obvious way. A common choice for the elementary edit-costs is
d(alpha,alpha)=0 d(alpha,beta) =2 if alpha!=beta ... cost of changing character alpha to beta d(alpha,-)=1 cost of deleting alpha d(-,alpha)=1 cost of inserting alpha and then d(a,b) = |a| + |b| - 2*|LCS(a,b)|
The LCS problem and the edit-distance problem find applications in computer-science and molecular-biology [8] [9] [10] [11] [12]. An LCS algorithm can compare two files and, by finding what they have in common, compute their differences. It can be used to correct spelling errors and to compare two genetic sequences for homology (similarity).
Under plausible assumptions [1] [13], the worst case complexity of an LCS or edit-distance algorithm on strings over an infinite alphabet must be O(|a|*|b|) time. Masek and Paterson [5] give an O(|a|*|b|/log(min(|a|,|b|))) edit-distance algorithm for strings over a finite alphabet with modest restrictions on d(.,.). However this is faster than simple algorithms only for strings longer than about 200,000 characters. For special cases there are faster algorithms: for similar strings [3] [6], and for strings with few matching characters [4], but their worst-case running time is at least O(|a|*|b|).
The algorithm presented here certainly has complexity O(|a|*|b|) for a finite alphabet, but asymptotically the improvement in speed is close to w. The algorithm is insensitive to the number of matches between strings and to their similarity.
1.1. Matrix L
Conventionally a matrix Lij is defined:
i^ | b3 - row3 j | b2 - row2 string b <-_____________| b1 - row1 ... a3 a2 a1 matrix Lij string a Lij equals the length of an LCS of a1..j and b1..i Lij = 1 + Li-1,j-1 if aj=bi = max(Li-1,j,Li,j-1) otherwise
This leads to simple dynamic-programming algorithms [8] upon which this one is based. A reflected representation of matrix L is typically used; the above representation is chosen to make the reading of certain bit-strings easier.
L has many interesting properties:
Li-1,j-1 <= Li,j-1, Li-1,j <= Lij, |Lij-Li-1,j-1| <= 1
The rows and columns of Lij contain ascending values for increasing i and j. This prompted Hunt and Szymanski [4] and Hirschberg [3] to "contour" L and develop fast algorithms for special cases.
2. Bit-String Algorithm
The values in the rows of L, increase by at most one. This makes it possible to represent the information in L by a bit-matrix:
#bits 10 0 1 0 1 1 0 0 0 1 0 1 1 1 1 1 1 | T string b 10 1 0 0 1 1 0 0 0 1 0 1 1 1 1 1 1 | G 9 0 0 0 1 1 0 0 0 1 0 1 1 1 1 1 1 | T 9 0 1 0 0 1 0 0 0 1 0 1 1 1 1 1 1 | T 8 0 0 1 0 0 0 1 0 0 0 1 1 1 1 1 1 | C 7 0 0 0 0 1 0 0 0 1 0 0 1 1 1 1 1 | T - row 11 7 1 0 0 0 0 0 0 1 0 0 0 1 1 1 1 1 | A - row 10 7 1 0 0 0 0 1 0 0 0 0 0 1 1 1 1 1 | G 6 0 0 0 0 0 1 0 1 0 0 0 0 1 1 1 1 | A 5 0 0 0 0 0 0 0 1 0 0 0 0 1 1 1 1 | A 5 0 0 0 0 1 0 0 0 0 0 0 0 1 1 1 1 | T 4 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 1 | T 3 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 | C 3 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 | G 2 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 | A 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 | T _________________________________. matrix Mij G T C T T A C A T C C G T T C G string a Lij = SIGMAk=1..j Mik Fig. 1.
Rowi has either the same number of bits set or one more bit set than the previous row, rowi-1. New bits are set towards the left of a row. The length of an LCS of 'a' and 'b' is the number of bits in the top row. The 1's in a particular row tend to drift to the right as we look (up) at the next row. This is because as more of 'b' is used, an LCS of a given length can be found using no more of, and possibly less of, 'a'. The 1's mark the contour lines of matrix L.
2.1 Alphabet-Strings
Each letter in the alphabet defines a bit-string when it is compared with the elements of 'a':
a: G T C T T A C A T C C G T T C G A-string: 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 C-string: 0 0 1 0 0 0 1 0 0 1 1 0 0 0 1 0 G-string: 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 T-string: 0 1 0 1 1 0 0 0 1 0 0 0 1 1 0 0
Precomputing these alphabet-strings contributes O(|alphabet|*ceiling(|a|/w)+|a|) to the time complexity. For a fixed alphabet this is O(|a|); for a non-fixed alphabet this could be O(|a|*|b|) at worst. If the alphabet is small, |alphabet|<<|b|, the contribution to the total time can be ignored.
2.2 Matrix M
To calculate rowi, we use the ith character in string 'b', bi, to select the bi-string from the set of alphabet-strings. The 1's in rowi-1 "cut" the bi-string into segments:
row10 : 1 0 0 0 0 0 0 1 0 0 0 1 1 1 1 1
T-string : 0 1 0 1 1 0 0 0 1 0 0 0 1 1 0 0
Each segment extends from the position of a 1 in rowi-1 rightward to the position to the left of the next 1. If the left-hand bit of rowi-1 is zero, the left-most segment extends from the left of the bi-string to the position left of the first 1. Rowi is formed by setting only the right-most 1 bits in each segment of the bi-string. If a segment is all zero, the bit defining the left end of the segment should be set in rowi (that is the segmenting bit in rowi-1). This can be ensured by first or-ing rowi-1 into the bi-string.
-
T-string Or row10:
* indicates a right-most 11 1 0 1 1*0 0 1 1*0 0 1* 1* 1* 1* 1*
row11: 0 0 0 0 1 0 0 0 1 0 0 1 1 1 1 1
It may be convenient to imagine an invisible 1 at position |a|+1 for a left-most segment which is zero, but this is unnecessary for the algorithm.
A 1 in rowi-1 marks the shortest piece of 'a' that can be used to make an LCS of a certain length with b1..i-1. Bringing bi into use, the best that can be done to extend that LCS is to use the first bi in 'a' to the left of the 1, if possible. This is marked by the right-most 1 bit in the next segment to the left.
In more detail, let x = rowi-1 Or bi-string.
eg. x = row10 Or T-string x: 1 1 0 1 1 0 0 1 1 0 0 1 1 1 1 1
Each segment of x can be read as a binary number. There is a "folk-technique" that decrementing a binary number changes the low-order bits [7] up to and including the least-significant 1. The correct decrement for each segment can be found by a logical left-shift of rowi-1 with a 1 carry-in:
x: 1 1 0 1 1 0 0 1 1 0 0 1 1 1 1 1 - 0 0 0 0 0 0 1 0 0 0 1 1 1 1 1 1 ------------- ------- - - - - - 1 1 0 1 0 1 1 1 0 1 1 0 0 0 0 0
A non-equivalence of the result and x sets the changed bits:
0 0 0 0 1 1 1 0 1 1 1 1 1 1 1 1
And-ing this with x gives the right-most bits in each segment:
0 0 0 0 1 0 0 0 1 0 0 1 1 1 1 1
This is rowi, row11 in this example.
In summary:
rowi = x And ((x - (rowi-1 << 1)) != x)
where x = rowi-1 Or bi-string
Or And != bit-string operations
<< logical left-shift bit-string; right-hand bit set
- |a|-bit integer subtraction
The bit-string operations can be done in units of a word-length. The shift and subtraction can also be done one word at a time, taking care that the carry-out-bit and the borrow-bit are propagated.
The number of bits set in a word can be counted in O(log2(w)) time; this is attributed to D.Muller in 1954 in [7]. The number of 1's in the final row therefore can be calculated in O(ceiling(|a|/w)*log2(w)).
2.3 An LCS
An LCS, as opposed to just its length, can be obtained in at least two ways. Hirschberg's recursive technique [2] can be used to find an LCS in linear-space at the cost of slowing the algorithm by a factor of two.
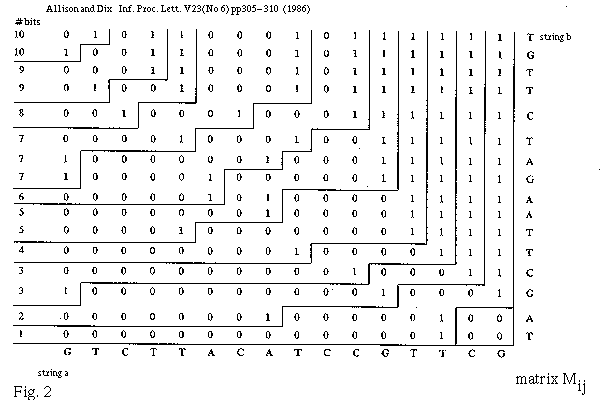
Alternatively all rows of M can be kept, the space required is |a|*|b| bits, ceiling(|a|/w)*|b| words. This is quite practical for strings of the order of 1000 characters. Then an LCS can be recovered by finding the "corners" of the contours in L which stand out as patterns in M (see Fig 2). This takes O(|a|+|b|) time. The emboldened characters in Gig. 2 indicate an LCS.
3. Simulation Results
|
The ('86 classic-) C-code can be found
[here]. |
Both the simple O(|a|*|b|) algorithm [2] [8] and the bit-string algorithm to calculate the length of an LCS have been implemented in C and run on a Vax-11/750 with a 32-bit word. For random strings and an alphabet of size 4 the resulting speedups were:
|a| * |b| Time Ratio (Simple/Bit) 32 * 32 6 64 * 64 10 100 * 100 11 500 * 500 25 1000 * 1000 26 4000 * 4000 27
For comparison, an alphabet of size 256 resulted in:
|a| * |b| Time Ratio (Simple/Bit) 32 * 32 2 64 * 64 5 100 * 100 6 500 * 500 19 1000 * 1000 21 4000 * 4000 27
A similar number of operations are in the inner loop of each algorithm. The bit-string algorithm is well suited to optimization since it works across rows of matrix M and alphabet-strings. For small alphabets, the bit-string algorithm clearly provides a considerable speedup.
4. Conclusions
The time complexity of the bit-string LCS algorithm on a computer with w-bit words for a fixed finite alphabet is
O( ceiling(|a|/w)*|b| )
This gives a speedup over simple O(|a|*|b|) algorithms. The time does not depend on properties of 'a' and 'b'. For random strings and moderate alphabets, the bit-string LCS algorithm will be faster than the special case algorithms.
The algorithm might also be programmed on a vector-computer if carry-out and borrow bits can be propagated from word to word in a vector-shift and a vector-subtract operation. It could be "pipelined" in a diagonal fashion on a vector or parallel machine because the least significant bit (or word) of rowi+1 can be calculated as soon as the least significant bit (or word) of rowi has been calculated.
References
[1] A.V.Aho, D.S.Hirschberg, J.D.Ullman. Bounds on the complexity of the longest common subsequence problem. JACM Vol.23 No.1 pp.1-12 1976.
[2] D.S.Hirschberg. A linear space algorithm for computing maximal common subsequences. CACM Vol.18 No.6 pp.431-343 1975.
[3] D.S.Hirschberg. Algorithms for the longest common subsequence problem. JACM Vol.24 No.4 pp.664-675 1977.
[4] J.W.Hunt, T.G.Szymanski. A fast algorithm for computing longest common subsequences. CACM Vol.20 No.5 pp.350-353 1977.
[5] W.J.Masek, M.S.Paterson. How to compute string-edit distances quickly. in Time Warps, String Edits and Macromolecules: The Theory and Practice of Sequence Comparison. D.Sankoff, J.B.Kruskal eds. Addison-Wesley 1983.
[6] N.Nakatsu, Y.Kambayashi, S.Yajima. A longest common subsequence algorithm suitable for similar text strings. Acta Informatica Vol.18 pp.171-179 1982.
[7] E.M.Reingold, J.Nievergelt, N.Deo. Combinatorial Algorithms: Theory and Practice. Prentice Hall 1977.
[8] D.Sankoff, J.B.Kruskal eds. Time Warps, String Edits and Macromolecules: The Theory and Practice of Sequence Comparison. Addison-Wesley 1983.
[9] P.H.Sellers. On the theory and computation of evolutionary distances. SIAM Jrnl of Math' Vol.26 No.4 pp.787-793 1974.
[10] P.H.Sellers. The theory and computation of evolutionary distances: pattern recognition. Jrnl of Algorithms Vol.1 No.4 pp.359-373 1980.
[11] R.A.Wagner, M.J.Fischer. The string-to-string correction problem. JACM Vol.21 No.1 pp.168-173 1974.
[12] M.S.Waterman. General methods of sequence comparison. Bulletin of Math' Biology Vol.46 No.4 pp.473-500 1984.
[13] C.K.Wong, A.K.Chandra. Bounds for the string editing problem. JACM Vol.23 No..1 pp.13-16 1976.
NB. The C-code and an interactive demonstration are [here].
* as of 2005: Faculty of Information Technology (Clayton School), Monash University, Victoria 3800, Australia.
* as of 2001: School of Computer Science and Software Engineering, Monash University, Victoria 3168, Australia.
L. Allison & T. I. Dix. A Bit-String Longest-Common-Subsequence Algorithm. Inf. Proc. Letters, Vol.23, pp.305-310, Dec. 1986.
Some later literature refers to 'bit vectors' and/or applies them to edit distance (approximate matching) v. longest common subsequence (LCS, LCSS) problems but the technique remains very similar.