To align two or more sequences is to pad out each sequence with null "characters", ‘-’, until they have the same length and in such a way as to optimise some criterion -- to maximise a score or to minimise a cost. The sequences can then be written out one above the other, e.g.,

  S1: ACGTA-GTACGT
      || || ||| ||
  S2: AC-TACGTAGGT

If you care to think of S1 as the ancestor and of S2 as the descendant then a ‘-’ in S2 indicates a deletion and a ‘-’ in S1 indicates an insertion; insertions and deletions are collectively called indels. However you can just as well consider S2 to be the ancestor and S1 the descendant. If S1 and S2 are present day sequences related by evolutionary history then they are both descendants of some unknown hypothetical ancestor.

Generally, a match (identical characters) is "good" and has a high score (low cost), and mismatch, insertion & deletion are "bad" and have low scores (high costs).

An alignment that optimises the criterion is optimal. An optimal alignment can be found with a dynamic programming algorithm [DPA]. In general, there may be more than one optimal alignment, even a great many.

If there are more than two sequences to align, the process is called [multiple alignment]. There are various ways of defining a score function or a cost function on multiple alignments. Alignment of [three sequences] is a useful special case because each internal node of a [phylogenetic tree] (evolutionary tree) has three neighbours.

Alignment Probability Density

In general there can be a great many optimal and near optimal alignments. It may be impossible to say which is the correct one; the data may not justify selecting a single one. It is possible to calculate an alignment probability density plot, e.g.,

Chicken hemoglobin α chain v. β chain,
CHKHBAM[120..195] (top) v. CHKHBBM[170..255] (left),
three-state machine (linear costs),
alignment probability density plot,
J. Molec. Evol., 35(1), pp.77-89, 1992
[doi:10.1007/BF00160262].

Such probabilistic alignment plots show the degree of uncertainty in a problem.

It is also possible to sum the probability of all alignments (still in O(|S1|*|S2|)-time) and answer the question of whether S1 and S2 are related or not, even in the "grey zone" of distantly related sequences. Even when no single alignment is statistically acceptable, their sum may be.

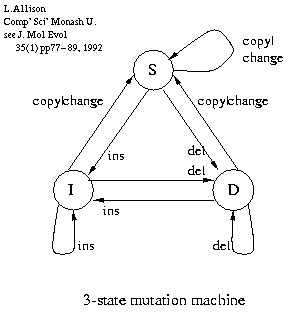
Modelling Gap Costs

Probabilistic finite state machines (automata), also sometimes called (pair) hidden Markov models (HMM, PHMM), can be used to model different kinds of 'gap costs'.

A one state machine models simple gap costs.

A three state machine (right) models linear (affine) gap costs. It lets us have a lower probability of starting a gap and a higher probability of continuing that gap, and when logs are taken we get a cost (message length) that is linear in the length of the gap.

A five state machine models piecewise linear gap costs, and so on.

If the model's parameters are not known in advance, they can be fitted to the data sequences (also see 'bias' below). If i>j, an i-state machine is a more complex hypothesis than a j-state machine and is almost certain to fit the data better. MML is used to include the cost of a model in an inference and thus prevent overfitting.

Unequal Symbols

Not all symbols (bases or amino acids) are created equal. For example, Plasmodium falciparum is ~80% AT-rich, so a C or a G is much rarer than an A or a T, and is worth much more ( - log 0.1 v. - log 0.4). The probability of a symbol can also depend on the context. For example, an A can be much more likely after a run of As, ...AAA<?>, or after ...TAT<?>. The alignment and the [compression] of sequences can be combined to model such effects and produce better alignments, as in [M Align] (also see modelling alignment).

Bias in Distance Estimates

Note that optimal aligments give biased estimates of the parameters of evolutionary distance and relatedness, particularly for distant relationships, but average alignments give unbiased estimates [Bioinf], [JME].