Phylogenetic Trees

Input: Usually k DNA, or protein, sequences, S₀, ..., S_k-1; let n be the average length.

The sequences may be pre-aligned. This may be to reduce the problem's computational complexity, or it may be argued (rationalised?) that the true alignment is known by other means, say from protein structure alignment. (But also see the mutual dependency of trees and alignments, below.)

If aligned, columns containing nulls, '-', may have been deleted. The '-' is not a regular symbol and must not be treated like one.

Output: An evolutionary tree.

The tree can be an unrooted- or rooted-tree.

Generally, each given sequence is a leaf of the tree, and each internal node represents a hypothetical, unknown, ancestral sequence.

It can be that a single tree is excessively 'precise'; there may be several acceptable trees between which the data cannot distinguish.

k	2	3	4	5	6	...
#	1	1	3	15	105	...

There are 1×3× ... ×(2k-5) unrooted trees with k leaves, k≥3 (k-2 internal nodes each of degree 3, 2k-3 edges).

Note that each internal hypothetical node of an unrooted tree has three neighbours, so iterated three-way alignment may be useful.

(An unrooted tree can be turned into a rooted tree by adding a root node on some edge, picking the tree up by this root, and giving it a good shake.)

As well as its 'topology', the tree may have one or more parameters per edge -- time, probability(ies) of mutation(s), probability of indel, ..., as appropriate. The parameters may be independent, edge to edge, or not, depending on the model.

There is little point in considering rooted trees unless you also consider a molecular clock and a (fairly) constant rate of mutation. In principle, a rooted tree has about half the number of edge parameters of an unrooted tree.

Almost invariably a rooted tree is a (rooted) binary tree, although allowing more general trees would be one way to reduce some of the 'precision' of the inference.

In reality, an evolutionary tree and a multiple alignment are mutually dependent. The tree depends on the multiple aligment and v.v..

An evolutionary tree, with edge parameters, implies a cost function, and hence a rank-ordering on multiple alignments.

Changing the tree may change the rank-order of alignments, and changing the alignment may change the rank-order of trees.

Note that optimal alignment gives biased estimates of evolutionary distance [Bioinf] [JME]; average aligments (e.g., by sampling, see below) are unbiased.

Naive multiple alignment takes O(n^k)-time; searching for an optimal tree and alignment, both together, is a doubly hard problem.

Stochastic search (for tree, or alignment, or both) can be a partial way around the computational complexity (besides yielding the variation of parameter estimates).

Other Points:

Order-preserving global alignment becomes less appropriate for long sequences, esp. for genomes, and order-preservation should be relaxed, at least partially.

Recombination and horizontal gene transfer (HGT) introduce non-tree edges. The search problem gets harder.

Optimisation criteria:

Parsimony: Find the tree (and alignment) that implies the minimum total number of mutations, e.g., S₀="A...", S₁="A...", S₂="C...", S₃="C...", then ((S₀,S₁),(S₂,S₃)) ⇒ 1+..., but ((S₀,S₂),(S₁,S₃)) ⇒ 2+... . The model is that all mutations on all edges are equally probable, which seems implausible in general. (I argue that the first M, in MML, is the true meaning of parsimony.)

Maximum Likelihood: Find the tree, T, with edge parameters, (and alignment) that maximises pr(S₀,...,S₀ | T).

Minimum Message Length (MML): A Bayesian criterion. Find the tree, T, with edge parameters, (and alignment) that minimises the information of the tree plus the sequences given the tree, I(T) + I(S₀,...,S₀ | T). Note that the edge parameters, and even the tree topology, should be stated to (only) optimum 'precision'.

Distance Matrices: Given a pairwise distance matrix, M_i,j = d(S_i, S_j), find the two closest sequences, remove them, and replace them by their 'ancestor'. Repeat until two entries (unrooted), or one (rooted) entry, remain(s). Each new ancestor must come with distances to the remaining sequences.
This is a tree building method, not an optimisation criterion like the others. Its attraction is that there are "only" ^kC₂ pairs of sequences and an entry can be computed "fairly" quickly, in a variety of ways, even for long sequences. The drawback is that the method relies on the distance being ~ time, and on there being a constant rate of mutation.

Search Methods

Exhaustive: n will be "short", and k "few".

Greedy, e.g., pair-wise bottom-up, but errors and ambiguities tend to accumulate.

Heuristics (arguably includes distance matrices).

4-mers: For each subset of 4 sequences, find the best of the 3 unrooted trees over the subset. Find a complete tree consistent with all or many of the small trees.

DFT, discrete Fourier transform method!

Stochastic, e.g., perturb the tree (find a T₄ and replace it with one of the 2 alternatives), accept or reject probabilistically, repeat many times. Can 'sample' average trees, or 'cool' towards an optimal tree.

Edge Parameter Estimates

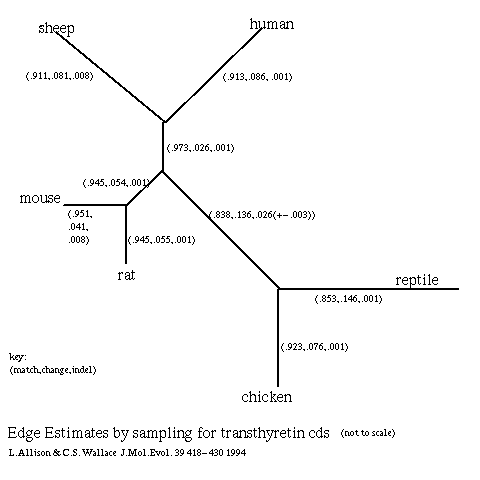
Transthyretin (Duan et al 1991, Schreiber et al 1992) is a protein expressed in the brain and also expressed in the liver of some animals. There is little doubt about the correct topology of the phylogenetic tree for the six sequences used; the edge estimates (below) were obtained by Gibbs sampling (Allison & Wallace) over 1000 multiple alignments for this tree: