Minimum Message Length Encoding, Evolutionary Trees and Multiple-Alignment.
Appears in Hawaii Int. Conf. Sys. Sci. 25, Vol.1, pp.663-674, January 1992
L. Allison, C. S. Wallace and C. N. Yee,
Department of Computer Science, Monash University, Australia 3168.
Abstract: A method of Bayesian inference known as minimum message length encoding is applied to inference of an evolutionary-tree and to multiple-alignment for k>=2 strings. It allows the posterior odds-ratio of two competing hypotheses, for example two trees, to be calculated. A tree that is a good hypothesis forms the basis of a short message describing the strings. The mutation process is modelled by a finite-state machine. It is seen that tree inference and multiple-alignment are intimately connected.
Q: What is the difference between a hypothesis and a theory?
A: Think of a hypothesis as a card.
A theory is a house made of hypotheses.
(From rec.humor.funny, attributed to Marilyn vos Savant.)
Keywords: inductive inference, minimum message/ description length, multiple-alignment, evolutionary-tree, phylogenetic tree.
1. Introduction.
In previous papers[1, 2], minimum message length (MML) encoding was used to infer the relation, if any, between 2 strings and to compare models of mutation or relation. Here we apply MML encoding to the problems of multiple-alignment and inference of an evolutionary-tree given k>=2 strings of average length n. MML encoding is a method of Bayesian inference. We consider the message length of an explanation of given data D. An explanation consists of a message which first states a hypothesis H, then states the data using a code which would be optimal were H true. It is a basic fact of coding theory that the message length (ML), under optimal encoding, of an event of probability p is -log2(p) bits. From Bayes' theorem in the discrete case:
P(H&D) = P(H).P(D|H) = P(D).P(H|D) ML(H&D)= ML(H)+ML(D|H)= ML(D)+ML(H|D)
P(D|H) is called the likelihood of the hypothesis. It is a function of the data given the hypothesis; it is not the probability of the hypothesis. P(H) is the prior probability of the hypothesis and P(H|D) is its posterior probability. If ML(H) and ML(D|H) can be calculated for given H and D then the posterior odds-ratio of 2 hypotheses can be calculated. Analogous results hold in the continuous case and imply an optimum accuracy for estimating real-valued parameters, although the calculations can be difficult. MML encoding can be used to compare models, test hypotheses and estimate parameters. Wallace and Freeman[25] give the statistical foundations.
Maximum-likelihood methods and MML encoding are related. A significant difference is that the former do not cost the model or hypothesis complexity, ML(H), and so tend to favour overly complex or detailed models. In sequence analysis the issue covers: the estimation of parameters to optimal accuracy, the complexity of models of mutation and of evolution and the fact that a single alignment is too precise a hypothesis. In cases where model complexity is constant, it can be ignored and then maximum-likelihood and MML encoding give the same results.
We next link inference over 2 strings to problems over k strings. Given strings A and B, the following questions can be raised:
Q1: Are they related?Q2: Are they related by a particular model of relation and parameter values (~ time since divergence)?
Q3: Are they related by a particular alignment?
Q4: Are they related by descent from a particular common ancestor?
An answer to one of these questions can "only" be a hypothesis. An explanation of the strings can be based on such an answer. Explanations based on successive questions carry increasing amounts of information and must have increasing message lengths. A and B have infinitely many possible common ancestors. It is possible to dismiss most as wildly improbable but impossible to identify a common ancestor with certainty without extra information. An alignment implies a subset of possible ancestors in a natural way. Conventional alignment programs return a single alignment which is optimal under some explicit or implicit assumptions - a model. A given model can relate A and B by many different alignments and we call the answer to Q2 the r-theory (for relation). It states the inferred parameters for the evolution of A and B followed by A and B in a code based on all possible alignments. A by-product is a probability density plot of all alignments. The answer to Q1 would require the sum over all models of the integral over all parameter values. This calculation is impractical and the result would be of little use; Q2 is the question usually asked.
There is a natural null-theory in sequence analysis. If the strings are unrelated, it is not possible to do better than transmit them one after the other, at about 2 bits per character for DNA. The lengths of the strings must also be transmitted. Any explanation that has a message length greater than that of the null-theory is not acceptable.
The approach to problems over 2 strings
generalises to problems over k>=2 strings.
Questions analogous to Q1-Q4 arise
when given k strings which might be related by an evolutionary-tree:
R1 (a): Are
they related or, slightly more detailed,
R1 (b): are
they related by a particular tree-topology?
Consideration is usually restricted to binary trees
and we follow this convention here.
It is not hard to allow arbitrary branching factors.
Forests should be allowed so as to permit independent families;
the message length
of a forest includes the sum of those of its trees
and the generalisation is obvious.
R2: Are they related by a particular tree
(topology + parameter values for each edge).
Each edge of the tree represents a simple 2-string relation
and the inferred parameters for each edge (~ time) are required.
This is the generalised r-theory.
R3: Are
they related by a particular multiple-alignment?
R4: Are
they related by descent from particular ancestors?
The chain Q1:Q2:Q3:Q4 matches the chain R1:R2:R3:R4 and in particular Q2:Q3 matches R2:R3, although this requires some discussion. Many misunderstandings come from confusing answers to R3 with those to R2. A tree (topology & edge parameters) implies a probability distribution on character-tuples and thus on multiple-alignments. The probability of a tree and the strings (R2) is the product of the prior probability of the tree and the sum of the probabilities of all such multiple-alignments given the tree. When k>2, the number of alignments is very large and heuristics are needed to make the computations feasible. R3 can be taken in 2 ways. We take the word `related' to mean `related by an evolutionary-tree'. A tree has 2k-3 edges and thus has O(k) parameters but there are 5k-1 possible tuples in a multiple-alignment. There is a smaller but still exponential number of `patterns'. Many of the tuples' probabilities are locked together under an evolutionary-tree hypothesis. If `related' were taken to mean any arbitrary relation, there would be more degrees of freedom in the form of hypotheses which might enable the data to be fitted better but at the higher overhead of stating more parameters.
Reichert et al[21] were the first to apply compact encoding to the alignment of 2 strings. They used one particular model of relation and sought a single optimal alignment. This was difficult to do efficiently for the model that they chose. Bishop and Thompson[5] defined maximum-likelihood alignment for what is a 1-state model although they recognised the possibility of other models. Allison et al[2] objectively compared 1, 3 and 5-state models of mutation using MML encoding. Felsenstein[11,12] developed a maximum-likelihood method for inferring evolutionary-trees. To date, it is the method with the soundest statistical credentials. His program does not do alignment itself and requires a multiple-alignment as input. Friday[13] discussed the problem of assigning figures of merit to inferred trees. Wallace and Boulton developed MML methods for classification[24,7], and for hierarchical classification[8], of arbitrary "things". In classification, a class usually contains many things. Cheeseman and Kanefsky[9] applied MML encoding to evolutionary-trees over macro-molecules. Milosavljevic[20] examined the MML classification of macro-molecules.
The methods described in this paper relate to other methods as follows. They generalise Felsenstein's approach by allowing inserts and deletes to be inferred and by including the cost of the model. In contrast to Cheeseman and Kanefsky, ancestral strings are not inferred, for to do so involves arbitrary choices. However probabilities can be assigned to possible ancestors and to possible alignments given the parameters that are inferred.
string A= TAATACTCGGC string B= TATAACTGCCG mutation instructions: copy change(ch) NB. ch differs from the corr' char in string A. del ins(ch) a mutation sequence: copy; copy; delete; copy; copy; ins(A); copy; copy; del; copy; change(C); copy; ins(G) generation instructions: match(ch) mismatch(chA,chB) NB. chA<>chB insA(chA) insB(chB) a generation sequence: match(T); match(A); insA(A); match(T); match(A); insB(A); match(C); match(T); insA(C); match(G); mismatch(G,C); match(C); insBG equivalent alignment: TAATA-CTCGGC- || || || | | TA-TAACT-GCCG
Figure 1: Basic Models.
2. Mutation-Models.
We consider 2 broad models to relate 2 strings A and B (Figure 1). In the mutation-model a simple machine reads string A and a sequence of mutation instructions and outputs string B. In the generation-model a simple machine reads a sequence of generation instructions and outputs strings A and B on a single tape 2 characters wide. There is an obvious correspondence between a mutation sequence, a generation sequence and an alignment. Results based on these notions are equivalent and they can be used interchangeably as convenient.
The machines that we consider are probabilistic finite-state machines as described in [2]; they are equivalent to hidden Markov models. We usually consider symmetric machines where p(ins) = p(del) = p(insA) = p(insB). The message length of an instruction is -log2 of its probability plus either 2 bits for 1 character or log2(12) bits for 2 differing characters; for simplicity only, we assume that all characters are equally probable. In highly conserved sequences, the probabilities of those instructions that do not conserve characters are low and their message lengths are high. The probability of an instruction also depends on the current state, S, of the machine:
ML(match(c)|S) = -log2(P(match|S)) + 2 ML(mismatch(c,c')|S) = -log2(P(mismatch|S)) + log2(12) ML(insA(c)|S) = ML(insB(c)|S) = -log2(P(insA|S)) + 2
A 1-state machine corresponds to Sellers' edit distance[23] with adjustable weights. A 3-state machine can correspond to linear indel costs or weights. Machines with more than 3 states can correspond to piece-wise linear indel costs. Multiple states allow an instruction to have different probabilities in different contexts. eg. For a 3-state machine a run of indels can have a higher probability of continuing than of beginning, giving a linear message length or cost as a function of run length.
A message based on one generation sequence (or alignment) states: (i) the parameter values of the machine which give its instruction probabilities and (ii) the sequence of instructions. The parameters are estimated by an iterative process: Initial values are chosen and an optimal sequence found. An optimal code for this sequence should be based on probability estimates derived from the observed frequencies of instructions. This change in the parameter values cannot increase the message length but can make another sequence optimal, so iteration is necessary and is guaranteed to converge. A few iterations, typically 4 to 8, are sufficient for convergence. The process could find only a local minimum in theory but this is not a problem in practice. The parameters must be stated to an optimum accuracy; the instructions are chosen from a multi-state distribution and Boulton and Wallace[6] give the necessary calculations.
The r-theory (Q2) is based on all instruction sequences. The algorithms[2] that compute the r-theory for the various machines are dynamic programming algorithms [DPA] that perform <+,logplus> on message lengths in the inner step or <*,+> on probabilities, instead of the usual <+,min> on edit distances or <+,max> on lengths of common subsequences. (logplus(log(A), log(B)) = log(A+B)) The iterative process is used to estimate the parameter values based on weighted frequencies.
TATAA TA-TAA T-ATAA || | || || | || | TAATA 2 TAATA- 2 TAAT-A 2 etc. -CGGC CGGC- CGGC | | | | GCCG- 3 -GCCG 3 GCCG 4 --CGGC CGGC-- CG-GC- || || | | GCCG-- 4 --GCCG 4 -GC-CG 4 -CGGC- | | GC--CG 4 etc
Figure 2: Possible Sub-alignments.
Results reported in [2] support the widely held view that the 3 and 5-state machines are better models for DNA than the 1-state machine. The 3 and the 5-state machines have increasing numbers of parameters to be stated. This tends to increase the message length, but is more than made up for by a saving on the strings. There are practical difficulties in going beyond about 5-states. We do not yet have enough data to reliably judge between the 3 and 5-state machines. Traditionally, alignment programs have been based on Sellers' metric[23], or on linear and piece-wise linear cost functions for indels[14,15], or on arbitrary concave cost functions[19]. Some of these programs have several parameters requiring ad-hoc adjustments. MML encoding provides an objective way to compare models of differing complexities and to infer their parameter values.
We now examine the questions Q1-Q4 informally on the example strings
A = TAATACTCGGC and B = TATAACTGCCG.
Note, results on short strings
must be taken with a pinch of salt
and we use the 1-state model only because it is the simplest to discuss.
Q1: Are strings A and B related?
They probably are related but
it is hard to see exactly how.
They have at the least diverged considerably.
Q2: How far and in what ways have A and B diverged?
The front sections, TATAA:TAATA can be
related in several ways involving either
2 mismatches or 2 indels.
The central CTs probably match.
The end sections, GCCG:CGGC,
can be related with 2 indels and a mismatch,
or 4 indels or 4 mismatches.
On average we expect about 7 matches,
1 or 2 mismatches and a few indels.
Q3: What is the best alignment?
It is only possible to say that
it probably fits the scheme
T[A:AA]T[AA:A]CT[GCCG:CGGC] (Figure 2).
As noted, the 1-state model was used only for simplicity.
The 3 and 5-state models would penalise isolated indels more heavily.
Q4: What was the most recent common ancestor of A and B? It is only possible to say that it probably fits the pattern TA[A]TA[A]CTalpha where alpha involved 2 to 4 Cs and/or Gs.
T A T A A C T G C C G * - - . T: - * - - . . A: - # * + - . . A: . - * + + - - . . T: . - * * - - - . . A: . . - # * - - - . C: . . - + * + - - . T: . - + + * # + . . C: . . . + # + # + . G: . . - + # # # + G: . . + # + # C: . . + # * 1-state machine key: * # + - . MML plus: 0..1..2..4..8..16 bits 1 avg algn = 64.9 bits null-theory = 56.0 bits r-theory = 53.8 bits = : <> : indel = 7 : 1 : 5.9 probability related = 0.8
Figure 3: Probability Density Plot.
When the r-theory algorithm is run on strings A and B the results (Figure 3) quantify the informal arguments made above. The optimal alignments stand out in the density plot but there are several of them and many other near-optimal alignments. Any 1 alignment has a message length greater than the null-theory and is not acceptable but taking them all together the r-theory is acceptable.
3. Trees over Two Strings.
Given 2 related strings A and B, we think of them as having evolved from a most recent common ancestor P.
P . . MA. .MB . . A B
Figure 4: Common Ancestor.
This involves 2 unknown steps or mutation machines, MA and MB (Figure 4). The models are reversible and mutating P into A by MA is equivalent to mutating A into P by MA'. The composition of 2 s-state machines MA' and MB is not in general equivalent to an s-state machine for s>1. Fortunately, for typical overall indel rates a single s-state machine is a good approximation to the composition of 2 or more s-state machines. It is thus acceptable to relate A and B directly by a single s-state machine. For example, Figure 5 plots -log2 probability of indel length for the composition of 1, 2 and 512 machines, for machines that can cause short (s) or long (L) indels and that give asymptotically piece-wise linear costs.
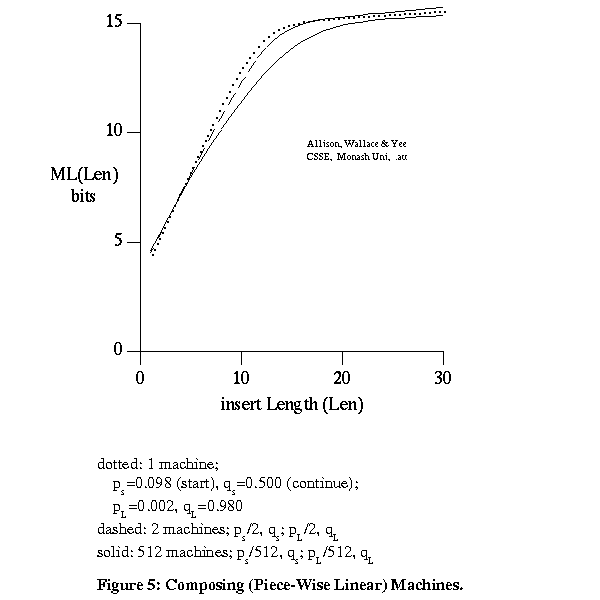
The calculations are based on machines that can copy or insert only. The similarity of form of the curves is important, not their absolute values. This also suggests that when considering any 2 out of k strings, and the path of machines (edges) between them in a tree, in order to get partial information on a multiple-alignment, it is acceptable to combine 2 or more adjacent s-state machines into one.
Note that there are 2 forests over A and B. The r-theory tree (Figure 4) forms 1 forest. The forest of 2 singleton trees corresponds to the null-theory.
If the ancestor P and the mutation instruction sequences that MA and MB executed were known, it would be possible to form an equivalent generation sequence (Figure 6) for a single generation machine G. However neither P nor the mutation sequences are known. The idea to circumvent this problem is to synchronise MA and MB as they read P and to remove dependency on the unknown P by summing over all possibilities. MA and MB are forced to execute copy, change and delete instructions in parallel; each of these instructions reads 1 character from P. Equivalently, G executes a match, mismatch, insA or insB instruction as appropriate except that if both MA and MB execute a delete, G does nothing. Note that an insert reads no character from P. If MA is about to execute an insert instruction and MB is about to execute some other kind of instruction, MB is delayed and G executes an insA, and v.v. If both MA and MB are about to execute 1 or more inserts, they and G can be made to do one of several things; double-counting can be avoided if this is done carefully.
Instruction. Explanations and Rates. match(x): x x x<---x--->x x<---y--->x pA'(c).pB'(c) pA'(ch).pB'(ch)/3 mismatch(x,y): x y x<---x--->y x<---y--->y pA'(c).pB'(ch) pA'(ch).pB'(c) x<---z--->y pA'(ch).pB'(ch)2/3 insA(x): x _ x<---x--->_ x<---y--->_ pA'(c).pB'(d) pA'(ch).pB'(d) x<---_--->_ pA'(i) insB(x): _ x _<---x--->x _<---y--->x pA'(d).pB'(c) pA'(d).pB'(ch) _<---_--->x pB'(i) _ _ _<---x--->_ "invisible", pA'(d).pB'(d) not seen c-copy, ch-change, i-insert, d-delete define pA'(instn) = pA(instn)/(1-pA(i)) pB'(instn) = pB(instn)/(1-pB(i)) rates per character of P Note pA'(c)+pA'(ch)+pA'(d) = pB'(c)+pB'(ch)+pB'(d) = 1 sum rates = (1+pA'(i)+pB'(i)) = (1-pA(i).pB(i))/((1-pA(i)).(1-pB(i)))
Figure 6: Explanations for Generation Instructions.
The inserts can be interleaved in different ways, eg. G can execute an insA and then an insB or v.v. Each of these options corresponds to a part of an alignment. Some, such as an insA immediately followed by an insB are of low, but non-zero, probability and are not usually seen in alignments. For example, a single optimal alignment always explains a pair of characters <Ai,Bj> as `mismatch(Ai,Bj)' and never as `insA(Ai);insB(Bj)' and thus gives biased estimates.
We expect P, A and B to have the same number of characters on average if pA(i)=pA(d) and pB(i)=pB(d). However we expect the alignment to be longer than P, for a tuple is "gained" whenever MA or MB does an insert but a character is only "lost" when both MA and MB delete it. For this reason, rates of instructions per character of P, ie. pA' and pB' in figure 6, have a denominator of (1-pA(i)) or (1-pB(i)). The expected number of (visible and invisible pairs) in the alignment per character of P is 1+pA'(i)+pB'(i).
The above points are generalised to k strings in the next section. Note that null is a non-character, not a proper character. Similarly an edge with a null at each end represents a non-operation for a machine, introduced only to synchronise MA and MB.
The parameters of G could be calculated from those of MA and MB but neither P, MA nor MB are known. In this case parameter values for G can still be inferred from A and B under the r-theory. The values embody the weighted average over all possible P and instruction sequences for MA and MB. If a constant rate of mutation is assumed, MA=MB and it is possible to infer the parameters of MA. For 3 or more strings it is possible to get a 3-way fix on all hypothetical strings and estimate all machines without assuming a constant rate of mutation.
4. Trees and Multiple-Alignment.
Of the questions, R1-R4, over k>=2 strings, we consider R2 to be the most important with R3 a close second, to recap: R2: Are the strings related by a particular tree? R3: Are they related [under an evolutionary-tree] by a particular multiple-alignment?
The topology of the tree is important but of little use without the amount and form of mutation on each edge. Strictly, R3 is too detailed to judge a tree on but an optimal alignment is often useful. As for the 2-string case, an optimal multiple-alignment is not unique in general and even sub-optimal alignments may be plausible.
An MML encoding of the strings based on an answer to R2 or R3 consists of
(i) the value of k,
(ii) the tree topology,
(iii) the parameter values for each edge and either
(iv) the strings, based on an all alignments (R2) or
(iv') the strings based on 1 optimal alignment (R3).
The tree that best explains the strings
gives the shortest message length.
The difference in message lengths of 2 trees
gives -log2 of their posterior odds-ratio.
The most colourless assumption is that all topologies are
equally likely so part (ii) is of constant length, given k,
and is only needed for comparison with the null-theory.
A rooted tree can only be inferred if a (near) constant rate of mutation is assumed. If this assumption is not made, an unrooted tree is inferred.
R2 and R3 can be broken down into sub-problems:
S1: What is the best tree-topology?
S2: What are the parameters for each edge?
S3: What is the message length of a tuple?
S4: What is the message length of an alignment?
S5: What is the message length of the strings given the tree,
considering all alignments taken together? (R2)
S5': What is the message length
of the strings given the tree and based on 1 optimal alignment? (R3)
The answers to these sub-problems are not independent. The topology and parameter values define the tuple probabilities and thus the alignment probabilities and the plausibility of each tree. Two competing sets of answers to the sub-problems can be judged easily and objectively but finding the best answers is hard. On the other hand, algorithms for the sub-problems are largely independent and can be studied as such. A prototype program has been written for R3 based on one set of approaches to these problems. Some other possibilities have also been investigated. These are discussed below.
4.1. S1: Tree-Topology.
There are Uk unrooted tree topologies over k strings:
U2 = U3 = 1 Uk = 1.3.5. ... .(2k-5), k>=4
ML(topology)=log2(Uk)
The prototype program requires the user to specify one or more trees to be evaluated. Standard distance-matrix methods could be used to propose plausible topologies. The ideal distance is proportional to time. It is thought that the parameters derived from the 2-string r-theory give more accurate pair-wise distances than a simple edit-distance. Felsenstein[12] describes how local rearrangements can be used to find at least a locally optimal tree.
There is no great difficulty in allowing n-ary trees, except that there are more of them. Note that a multiple-alignment method that does not explicitly consider a tree nevertheless embodies an implicit model of relation of some kind, possibly a fixed tree.
4.2. S2: Edge Parameters.
Each edge of the tree relates 2, possibly hypothetical, strings and is represented by a machine. Any realistic machine requires at least 1 parameter (~time) to specify instruction probabilities. The parameter(s) of each of the 2k-3 machines must be included in the message. The instructions are chosen from a multi-state distribution and Boulton and Wallace[6] give the calculations for the precision with which to state their probabilities.
The prototype program is based on 1-state machines, each having 3 parameters - P(copy), P(change), P(indel) - and 2 degrees of freedom. No correlation between P(change) and P(indel) is assumed. MML encoding is invariant under smooth monotonic transformations of parameters so the probabilities are stated rather than being translated into a measure of time. If a constant rate of mutation were assumed, it would be sufficient to describe k-1 machines. This would permit an objective test of this much discussed hypothesis: There is a fall of approximately 50% in the cost of stating parameters but presumably a rise in the cost of stating the strings. An intermediate theory, based on a near constant rate of mutation is also possible, with different trade-offs.
An iterative scheme, similar to that used for 2 strings,
is used to estimate the parameter values of the machines (edges).
This is described later.
Actual machine parameters: copy change indel m1: 0.9 0.05 0.05 m2: 0.9 0.08 0.02 m3: 0.7 0.2 0.1 m4: 0.8 0.1 0.1 m5: 0.75 0.1 0.15 A A . . m1. .m3 . A:0.43 A:0.40 . .C:0.56 C:0.59. +---------------------+ . m5 . . . m2. .m4 . . C C Probable hypothetical characters. Prior tuple probability = 0.00027 Estimated operations carried out: copy change indel m1: 0.43 0.57 m2: 0.57 0.43 m3: 0.40 0.60 m4: 0.59 0.41 m5: 0.94 0.06 (Probabilities less than 0.01 omitted.)
Figure 7: Example, explanations for tuple ACAC.
4.3. S3: Tuple Costs.
Here we consider the tree topology and parameters to be fixed. The probability of an alignment depends on the probabilities of the k-tuples of characters forming it. Each tuple can be thought of as an instruction of a k-string generation machine that generates all of the k strings in parallel. This machine is implied by the 2-string machines on the edges of the tree. The probability of a tuple can be found by assigning its characters, possibly null, to the leaves of the tree and considering all explanations of the tuple. An explanation assigns values to the internal, hypothetical characters of the tree. This defines an operation on each edge and a probability can be calculated for the explanation. The probability of the tuple is the sum of the probabilities of all explanations and its message length is -log2 of its probability.
We first consider the case where the mutation-model on 2 strings is a 1-state model. Felsenstein[12] gave the necessary algorithm to calculate the probability of a tuple of characters given the probability of a change on each edge of the tree. It takes O(k . |alphabet|2) time per tuple. It can be used directly by allowing the possibility of indels. Care must be taken that only 1 insert is allowed per explanation of a tuple, as an insert begins a new tuple. The tuple's probability is computed in a post-order traversal of the tree. The probabilities of hypothetical characters and of machine operations, given the tuple, (Figure 7) are computed in a subsequent pre-order traversal. The program computes the probabilities of tuples as they are encountered and stores them in a hash-table for reuse. There is a considerable saving when n>>|alphabet|.
Sankoff and Cedergren[22] give an algorithm that finds the single most probable explanation for a tuple; this is too detailed a hypothesis in general and is another case where a max over probabilities should be replaced with a `+'. It gives a good approximation when all mutation probabilities are small and all edges are similar. In that case the complexity of their algorithm is only O(k) per tuple.
string A: - A - A - A string B: B - - B B - string C: C C C - - - 1 2 3 4 5 6
Figure 8: Indel Patterns, k=3.
The situation is complex when the model relating 2 strings has more than 1 state. The 3-state model, giving linear indel costs, is of particular interest. There are 2k-2 patterns of indels possible in a tuple (Figure 8). The k-string generation machine therefore has 2k-1 states. (2k-1 is also the number of neighbours that each cell depends on in a k-dimensional DPA matrix.) Each tuple can therefore occur in 2k-1 contexts with a different probability in each one. This is a serious problem unless a simplification can be found. There is some hope because the probabilities of instructions in these contexts are not independent as there are only O(k) free parameters in the tree.
4.4. S4: Alignment Message Length.
The multiple-alignment part of the message states the length of the alignment and the tuples in the alignment. The former is encoded under the log* prior. The message length of a tuple was given in the previous section. It is therefore easy to compare 2 alignments on the basis of message length; the hard part is to find a good one.
4.5. S5': Optimal Multiple-Alignment.
The dynamic-programming algorithm [DPA] can be naively extended to k strings to find an optimal multiple-alignment. The k-dimensional DPA matrix has O(nk) entries. Each entry depends on 2k-1 neighbours. If the mutation-model has 1 state, the extension is straightforward and the time complexity is O(nk.2k). "Only" O(nk-1) space is needed to calculate the value of the alignment. The nk factor becomes painful, in both time and space, for n>=200 and k as small as 3. It is necessary to reduce the volume of the DPA matrix that is searched to make the algorithms practical and there are a number of possible approaches.
Altschul and Lipman[4] devised a safe method to restrict the volume investigated for an edit-distance based on fixed tree-costs and also for other costs. (The tree-cost of a tuple is the minimum number of mutations required to give the tuple.) Pair-wise alignments are done first and used to delimit a volume that is guaranteed to contain an optimal multiple-alignment. However, no results are available to indicate how practical the method is for tree-costs. The method relies on the triangle inequality and might be applicable to MML calculations.
A related heuristic is to use alignment-regions as fuzzy strings. Pair-wise alignments are performed on sibling leaf strings. A threshold (in edit-distance or in message length) is applied to limit the area of each alignment. Fuzzy strings are aligned in the obvious way until a complete multiple-alignment is obtained. The method is fast if the threshold is tight but is not guaranteed to find an optimal alignment. We have done some experiments with such an algorithm using fixed tree-costs. With a threshold of +1, up to 8 strings of 200 characters can be aligned on a DEC-5000. The model of computer makes only a small difference to the practical limits for this kind of complexity.
Hein[16] gave a multiple-alignment algorithm which uses directed acyclic graphs (DAGs) to represent fuzzy ancestral strings. The algorithm is fast but an optimal alignment is not guaranteed. Fixed tree-costs are used but this is by no means necessary. The value of DAGs is that in sections where there is consensus between the strings, the effective number of neighbours of a cell in the DPA "matrix" is much reduced.
Long exact matches between strings are fast to find using hash-tables or suffix trees. Heuristics for multiple-alignment based on splitting the strings on a long exact match, ideally near their centres, are clearly possible.
The prototype program operates in 2 stages. During an initial post-order traversal, strings and then alignments are aligned recursively until a complete multiple-alignment is obtained:
procedure RA(var Result:Alignment; T:Tree); var Left, Right :Alignment; begin if leaf(T) then StringToAlignment(T^.s, Result) else RA(Left, T^.left); RA(Right, T^.right); Align(Left, Right, Result) end if end
The machine parameters are held constant, at some reasonable but otherwise arbitrary values, during the initial stage. An improvement stage follows; the complete alignment is projected onto subalignments which are realigned during another post-order traversal:
procedure Improve(var Algn :Alignment); var A, B :Alignment; ss :StringSet; procedure Im(T:Tree; var ss:StringSet); var ss1, ss2 :StringSet; begin if not leaf(T) then Im(T^.left, ss1); Im(T^.right, ss2); ss := ss1+ss2; Project(Algn, ss1, A, B); Align(A, B, Algn); if ss <> AllStrings then Project(Algn, ss2, A, B); Align(A, B, Algn) end if else {leaf(T)} ss := [T^.s] end if end; begin Im(T, ss) end
The machine parameters are continually reestimated during this stage. The overall process takes O(kn2) time and global optimality is not guaranteed. The improvement stage can be iterated. More research needs to be done on alignment strategies.
Note that if the mutation-model on 2 strings has 3 states, to model linear indel costs, the k-string generation machine has 2k-1 states and each entry in the DPA matrix has 2k-1 entries. This also adds a multiplicative factor of 2k-1 to the time complexity.
4.6. S5: Sum over all Alignments.
The part of the message that describes the strings proper is ideally based on all alignments. The number of bits required to state the strings is -log2 of the sum of the probabilities of all alignments. This can be computed by a <+,logplus> dynamic programming algorithm. It suffers from the same combinatorial explosion as finding an optimal alignment. Fortunately most of the probability is concentrated in a narrow region which raises hopes for a fast approximate algorithm. This has been used to implement a fast, approximate r-theory algorithm for 2 strings[2]. Feng[3] has performed experiments on 3 strings which give good results. First, probability density plots are calculated for pair-wise comparisons. A "threshold" is applied to give a small alignment region. The regions are projected into the DPA cube. The r-theory is calculated over this volume. A further approach that we intend to implement is to to sum over all alignments in a region within a distance `w' of a multiple-alignment found as described in the previous section.
Pairs of states must be considered at each transition if the generation machine has `s' states, So if linear indel costs are modelled, a multiplicative factor of (2k-1)2, or O(22k), is included. This is a severe problem unless a simplification or an approximation can be found.
4.7. Estimating Edge Parameters.
The probability of a tuple can be calculated, as described previously, if all edge parameters are known. An iterative scheme is used to estimate unknown parameters. It is a generalisation of the scheme used for 2 strings: Initial values are assumed and used to find an optimal alignment (say) and to compute its message length and hence that of the tree hypothesis. For each tuple, the frequencies of operations for each machine are calculated. These frequencies are accumulated and used to calculate the instruction probabilities for the next iteration. The new values cannot increase the message length of the alignment but they may cause another alignment to become optimal. This must reduce the message length further so the process converges.
A test program has been written to investigate the estimation process alone for the 1-state model. It assumes that a long and "perfect" alignment is known, tuples occurring with their predicted frequencies. It then estimates the true machine parameters from arbitrary starting values. Convergence is rapid. The message length usually converges to within 1% of the optimum value within 3 iterations. All parameters are reestimated simultaneously. Note that the perfect alignment would be sub-optimal! Its statistical properties could only derive from a weighted average over all alignments.
This test program is also used to calculate limits for an acceptable hypothesis based on a single alignment for asymptotically long strings where the overhead of stating parameter costs and string lengths can be ignored. The critical point is where the null-theory and the alignment have equal message lengths. For example, when the machines in a tree are all identical and P(change) = P(indel) then the following results are obtained:
k: 2 3 4 5 critical P(copy): 0.68 0.79 0.82 0.83
The critical values of P(copy) would be higher for short strings. They would be lower if the probabilities of all alignments were summed; recall that a single alignment is an answer to R3 not to R2. Empirical results for 2 strings are given in [1].
The estimation scheme described above has been built into the alignment program. It will also be used in any r-theory algorithm in which case weighted frequencies will be used for estimation. The programs do not correct for the "invisible" tuple which has a probability of approximately (k-2).p(del)3. This results in an underestimate of indels by a similar amount but this is considerably less than the accuracy with which parameters can be estimated.
Input: 4 - k acgtacgtacagt - string 1 actgtacgtacgt - 2 acgtactagct - 3 accgtactgagct - 4 ((1 2)(3 4)) - tree 1 ((1 3)(2 4)) - 2 ((1 4)(2 3)) - 3 Tree 1: M.L.=108 bits * estimate of parameters: mc1: 0.88 0.02 0.09 mc2: 0.88 0.02 0.09 mc3: 0.94 0.03 0.03 mc4: 0.81 0.02 0.17 mc5: 0.71 0.18 0.11 s1 s4 . . .m1 .m4 . m5 . .--------------. . . .m2 .m3 . . s2 s3 s1[1..]: ac--gtacgt-acagt s2[1..]: ac-tgtacgt-ac-gt s3[1..]: ac--gtac-t-ag-ct s4[1..]: acc-gtac-tgag-ct Tree 2: M.L.=113 bits Tree 3: M.L.=122 bits Null-Theory= 124.5 bits NB. all trees are unrooted. CPU time = 7 secs/tree (Pyramid)
Figure 9: Example Run.
4.8. Null-Theory.
The null-theory is that the k strings are not related. Its statement consists of (i) the value of k, (ii) the lengths of the strings and (iii) the characters in the strings. Part (iii) requires 2 bits per character for DNA if all characters are equi-probable. Part (ii) is potentially a large penalty over a tree hypothesis because the latter states only a single length - of an instruction sequence. A reasonable approach, which mitigates this penalty, is to transmit the total length of the strings, encoded under the log* prior, followed by the set of lengths under a k-nomial prior. The second part is short if the lengths are similar. This generalises the binomial distribution used for 2 strings in [2]. The total message length of the null-theory is therefore:
MLnull = -log2(P(k)) -log2(P(total)) -log2(P(length1,...,lengthk|total)) +total*2 where total=length1+...+lengthk
Any hypothesis that has a message length longer than that of the null-theory is not acceptable. The previous section included predictions of critical values of P(copy) for a single alignment, asymptotically long strings and some special trees. Extensive tests have not been done but when the alignment program is run on artificially generated data the results of the significance test are consistent with the predictions. In particular, random strings are always detected as being unrelated.
4.9. Results.
Figure 9 shows the results of the prototype program on a small example. All 3 trees are acceptable hypotheses but tree 1 is the most plausible by a significant margin. All trees are un-rooted. Note that little benefit is gained from the hash-table for such short strings.
s1: HUMPALA Human prealbumin (transthyretin) mRNA, complete cds s2: RATPALTA Rat prealbumin (transthyretin) mRNA, complete s3: MUSPALB Mouse mRNA for prealbumin s4: sheep Transthyretin cDNA s5: chicken TTR cDNA transthyretin s1-s4: Tree ((1 2)(3 4)): M.L.=3693 bits Tree ((1 3)(2 4)): M.L.=3661 bits Tree ((1 4)(2 3)): M.L.=3569 bits * Null-Theory = 4781 bits s1-s5: Tree ((1 4) (2(5 3))): M.L.=4846 bits Tree ((1 4) ((2 5)3)): M.L.=4844 bits Tree (((1 5)4) (2 3)): M.L.=4807 bits Tree ((1(4 5)) (2 3)): M.L.=4758 bits Tree (((1 4)5) (2 3)): M.L.=4750 bits* *incl: 16.6 length, 67.1 params, 4655.9 alignment Null-Theory = 6134 bits s5 | s1 |m5 s2 . | . .m1 | .m2 . m6 | m7 . s6-----s8-----s7 . . .m4 .m3 . . s4 s3 estimate of parameters: copy change indel mc1: 0.89 0.09 0.02 mc2: 0.84 0.04 0.12 mc3: 0.95 0.05 0.01 mc4: 0.88 0.08 0.05 mc5: 0.74 0.18 0.08 mc6: 0.96 0.04 0.00 mc7: 0.88 0.10 0.03 CPU time approx' 5 min/tree (sparc station).Figure 10: Transthyretin DNA/RNA sequences.
Figure 10 gives results on transthyretin DNA and RNA sequences[10]. The grouping ((human sheep) (mouse rat)) is favoured on those 4 sequences. Joining chicken to the edge between the 2 pairs is narrowly the best option.
There is still debate over the branching pattern of human, chimpanzee and gorilla in the evolutionary tree of the primates. Figure 11 shows results on some globin pseudo-gene sequences. They favour the grouping (gorilla (human chimp)) and are consistent with the conclusions of Holmes[18, Ch 13] on these sequences. First, the 3 trees over gorilla, human, chimpanzee and owl-monkey sequences were evaluated. Owl-monkey was a consistent outsider. The orangutan sequence was then added and 3 trees were evaluated.
5. Conclusions.
We have shown how to use MML encoding to infer evolutionary-trees and multiple-alignments. We have argued that these problems are intimately connected. The posterior probability of a tree depends on the sum of the implied probabilities of all multiple-alignments. In this we agree with the sentiment, but not the detailed methods, of Hogeweg and Hesper[17] that "the alignment of sets of sequences and the construction of phyletic trees cannot be treated separately." The use of a single multiple-alignment leads to an underestimate of the posterior probability of the tree hypothesis and a bias in the parameter estimates. Nevertheless it is a reasonable approach when the strings are similar and a prototype program of this kind has been written for the 1-state model.
The MML method can compute the posterior odds-ratios of competing hypotheses such as different trees. The evolutionary-tree hypothesis is explicitly built into the message. The existence of a natural null-theory leads to an in-built significance test. These remarks are qualified with `subject to the validity of the underlying model'. The MML method requires the model to be defined explicitly. In principle, 2 competing models can be compared objectively; this was done for 2 strings in [2].
1: GGBGLOP:Gorilla beta-type globin pseudogene 2: HSBGLOP:Human beta-type globin pseudogene standard; DNA; PRI; 2153 BP 3: PTBGLOP:Chimpanzee beta-type globin pseudogene standard; DNA; PRI; 2149 BP 4: ATRB1GLOP:Owl-monkey psi beta 1 globin pseudogene. 2124 bp ds-DNA 5: ORAHBBPSE:Orangutan bases 1593 to 3704 s1-s4: Tree ((1 2)(3 4)): M.L.=7241 bits Tree ((1 3)(2 4)): M.L.=7236 bits Tree ((1 4)(2 3)): M.L.=7197 bits* Null-Theory = 17193 bits Elapsed time ~50 min's (Sparc station) s1-s5: Tree (((1 2) 3)(4 5)): M.L.=8023 bits Tree (((1 3) 2)(4 5)): M.L.=8031 bits Tree ((1 (2 3))(4 5)): M.L.=7980 bits* *incl: 18.7 length, 98.8 params, 7852 alignment Null-Theory = 21426 bits Elapsed time ~50 min's (Sparc station) estimate of parameters: copy change indel mc1: 0.989 0.011 0.000 mc2: 0.994 0.004 0.003 mc3: 0.988 0.012 0.001 mc4: 0.868 0.087 0.045 mc5: 0.969 0.016 0.015 mc6: 0.996 0.001 0.003 mc7: 0.985 0.011 0.005 s1:GGB | |m1 m2 m6 | m7 m4 s2:HSB---s6---s7-------s8----------s4:ATR | | |m3 |m5 | | s3:PTB | s5:ORA
Figure 11: Primate Globin Pseudo-genes.
The biggest doubts about the model used are as follows. We have not, as yet, modelled different transition and transversion rates but this would be straightforward. It seems to be difficult to bring a multi-state model of mutation properly into multiple-alignment. Large mutation events, such as block transpositions, duplications and reversals, could be modelled easily but finding an optimal "alignment" would become even harder. Finally, what is completely lacking from our method and from most if not all sequence analysis programs is any model of the pressure of selection.
The program discussed above is written in Pascal and is available, free for non-profit, non-classified teaching and research purposes, by email (only) from: lloyd at bruce.cs.monash.edu.au. The alignment programs for 2 strings, based on 1, 3 and 5-state models of relation and discussed in [2] are written in C and are also available. A good work-station with floating point hardware is the minimum requirement for their use.
Acknowledgment: This work was partially supported by Australian Research Council grant A49030439.
6. References.
- [1] Allison L. & C. N. Yee. Minimum message length encoding and the comparison of macro-molecules. Bull. Math. Biol. 52(3) 431-453 1990.
- [2] Allison L., C. S. Wallace & C. N. Yee. Inductive inference over macro-molecules. AAAI Spring Symposium on A.I. & Mol. Biol. Stanford March 1990 (extended abstract), and TR 90/148 Dept. Comp. Sci. Monash University 1990 [HTML] (in full).
- [3] Allison L. & Du Xiaofeng. Relating three strings by minimum message length encoding (abstract). Genes, Proteins and Computers, Chester, April 1990.
- [4] Altschul S. F. & D. J. Lipman. Trees, stars and multiple biological sequence alignment. SIAM J. Appl. Math. 49(1) 197-209 1989.
- [5] Bishop M. J. & E. A. Thompson. Maximum likelihood alignment of DNA sequences. J. Mol. Biol. 90 159-165 1986.
- [6] Boulton D. M. & C. S. Wallace. The information content of a multistate distribution. J. Theor. Biol. 23 269-278 1969.
- [7] Boulton D. M. & C. S. Wallace. A program for numerical classification. Comp. J. 13 63-69 1970.
- [8]
Boulton D. M. & C. S. Wallace.
An information measure for hierarchic classification.
Comp. J. 16 254-261 1973.
- [9] Cheeseman P. & B. Kanefsky. Evolutionary tree reconstruction (extended abstract). AAAI Spring Symposium on the Theory and Application of Minimal-Length Encoding Stanford 35-39 March 1990.
- [10] Duan W., M. G. Achen, S. J. Richardson, M. C. Lawrence, R. E. H. Wettenhall, A. Jaworowski & G. Schreiber. Isolation, characterization, cDNA cloning and gene expression of an avian transthyretin: implications for the evolution of the structure and function of transthyretin in vertebrates. Euro. J. Biochem. to appear.
- [11] Felsenstein J. Evolutionary trees from DNA sequences: a maximum likelihood approach. J. Mol. Evol. 17 368-376 1981.
- [12] Felsenstein J. Inferring evolutionary trees from DNA sequences. Statistical Analysis of DNA Sequence Data. B. S. Weir (ed) Marcel Dekker 133-150 1983.
- [13] Friday A. Quantitative aspects of the estimation of evolutionary trees. Folia Primatol. 53 221-234 1989.
- [14] Gotoh O. An improved algorithm for matching biological sequences. J. Mol. Biol. 162 705-708 1982.
- [15] Gotoh O. Optimal sequence alignment allowing for long gaps. Bull. Math. Biol. 52(3) 359-373 1990.
- [16] Hein J. A new method that simultaneously reconstructs ancestral sequences for any number of homologous sequences when the phylogeny is given. Mol. Biol. Evol. 6 649-668 1989.
- [17] Hogeweg P. & B. Hesper. The alignment of sets of sequences and the construction of phyletic trees: an integrated method. J. Mol. Evol. 20 175-186 1984.
- [18] Holmes E. C. Pattern and Process in the Molecular Evolution of the Order Primates. PhD Thesis, Cambridge University, 1989.
- [19] Miller W. & E. W. Myers. Sequence comparison with concave weighting functions. Bull. Math. Biol. 50(2) 97-120 1988.
- [20] Milosavljevic A. D. Categorization of macro-molecular sequences by minimum length encoding. University of California at Santa Cruz, UCSC CRL 90-41 1990.
- [21] Reichert T.A., D. N. Cohen & K. C. Wong. An application of information theory to genetic mutations and the matching of polypeptide sequences. J. Theor. Biol. 42 245-261 1973.
- [22] Sankoff D. & R. J. Cedergren. Simultaneous comparison of three or more sequences related by a tree. Time Warps, String Edits and Macromolecules: The Theory and Practice of Sequence Comparison. D. Sankoff & J. B. Kruskal (eds) Addison Wesley 253-263 1983.
- [23] Sellers P. H. On the theory and computation of evolutionary distances. SIAM J. Appl. Math. 26(4) 787-793 1974.
- [24] Wallace C. S. & D. M. Boulton. An information measure for classification. Comp. J. 11 185-195 1968. [HTML]
- [25] Wallace C. S. & P. R. Freeman. Estimation and inference by compact coding. J. Royal Stat. Soc. B 49(3) 240-265 1987. [paper]
Also see [Bioinformatics] and [MML].