<Exp> ::= <Exp> + <Term> |

<Exp> - <Term> |

<Term>

<Term> ::= <Term> * <Factor> |

<Term> / <Factor> |

<Factor>

<Factor> ::= x | y | ... |

( <Exp> ) |

- <Factor>

A grammar for the concrete syntax of simple arithmetic expressions

Non-terminal symbols:

<Exp>, <Term>, <Factor>

Terminal symbols:

+, -, *, /, (, ), x, y, z, ...

Start symbol:

<Exp>

Production rules as above.

 

Note the following are meta symbols:

::= (read it as "can be replaced by")

-> is alternative notation for ::=,

|   (read it as "or by")

e.g. An <Exp> can be replaced by   <Exp> + <Term>   or by <Exp> - <Term>   or by   <Term>.

Note that the production (replacement) rules for <Exp>, <Term> and <Factor> are recursive. The rule for <Exp> states that an Expression is a list of Terms separated by `+' or `-' symbols. A Term is a list of Factors separated by `*' or `/' symbols. A Factor is a variable (x, y, ...), or a parenthesized sub-expression, or a unary `-' followed by a Factor.

The operators `*' and '/' bind more tightly to their operands than `+' and binary `-' because `*' and '/' appear in the rule for <Term>, closer to the operands (<Factor>). Unary `-' binds most tightly of all operators.

The rules for <Exp> and <Term> are left recursive. This is because `+', `-', `*' and `/' are left associative: `a-b-c' gives the same parse tree as `(a-b)-c', not `a-(b-c)'.

A grammar like this can be turned into a "recursive descent parser" (a program) by writing a routine for each non-terminal in the grammar. The routines call each other as specified by the replacement rules. Left recursion, that is a replacement that begins with a recursive non-terminal, must be removed so that the parser does not loop. A simple parser of this type can be found in [Parser.c (click)] or [*.java] or [exp.sml].

1. x+y*z:

<Exp> => <Exp> + <Term> => <Term> + <Term> => <Factor> + <Term> => x + <Term> => x + <Term> * <Factor> => x + <Factor> * <Factor> => x + y * <Factor> => x + y * z

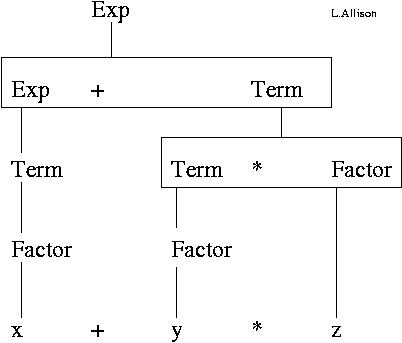
x+y*z: Full derivation-tree of non-terminals and replacements.

The result of parsing is often returned as a parse-tree based on a simpler abstract syntax. The abstract syntax corresponds to the datatype of parse trees returned by the parser.

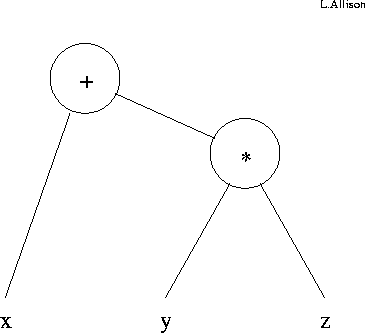
x+y*z: Parse tree.

2. (x+y)*z:

Parentheses '(' and ')' can be used to force a different parsing:

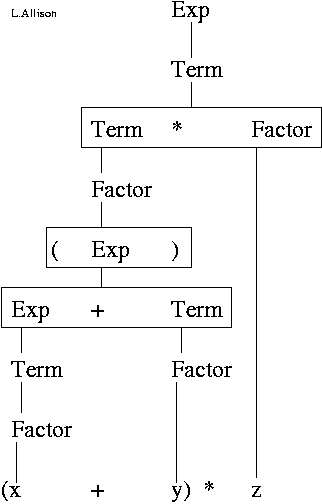
(x+y)*z: Full derivation-tree of non-terminals and replacements.

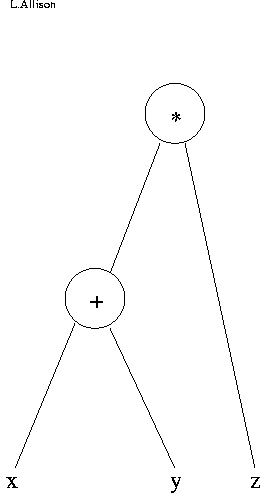
(x+y)*z: Parse tree.

Note that parentheses do not appear in any parse tree. They directed the parser to build a certain tree and after that they are unnecessary. The structure of the tree shows the binding of operators to operands without the need for (). Parentheses are only needed in strings.